简介
本文不是 PromptWizard 代码解读,而是来看 Prompt 是如何通过 meta prompt 一步步优化的。至于进化机制原理,大家都懂,不必啰嗦,重点关注 meta prompt。
框架
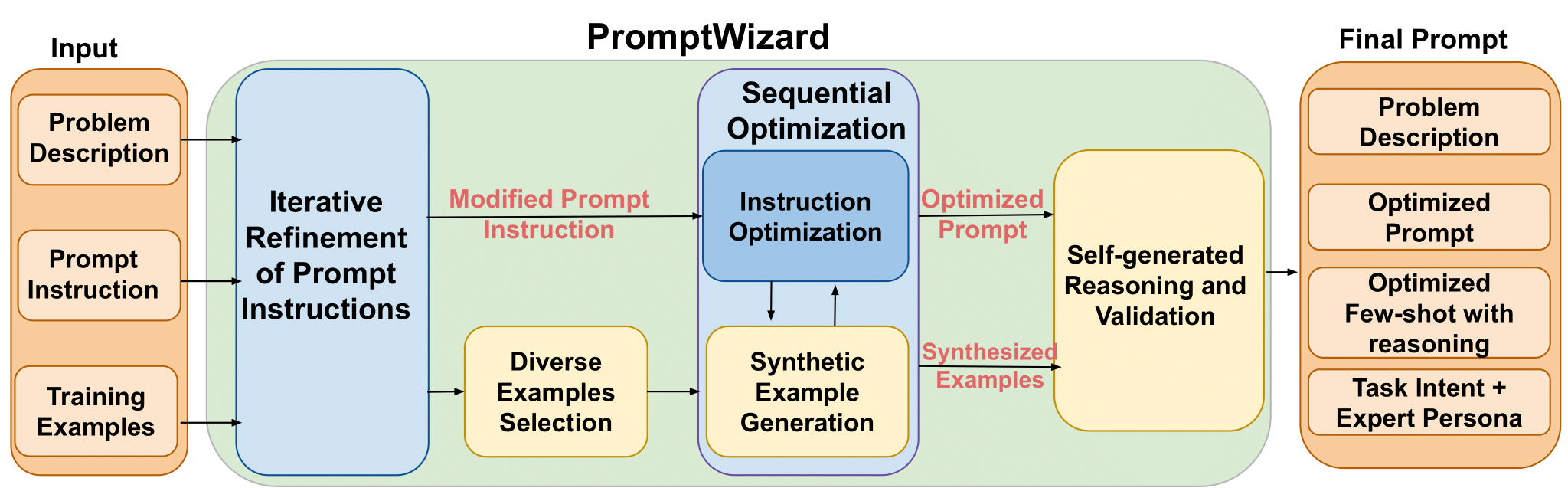
算法流程
Init
初始 Prompt:
task_description = You are a mathematics expert. You will be given a mathematics problem which you need to solve
base_instruction = Lets think step by step.
init_prompt = task_description + "\n" + base_instruction
注意到,初始 Prompt 并不是一个整体 Prompt,而是由 task_description 和 base_instruction 组成的。
system_prompt:
You are a helpful assistant developed by OpenAI that can efficiently perform tasks as per instruction
参数配置:
Prompt Optimization parameters: [('answer_format', 'For each question present the reasoning followed by the correct answer.'), ('base_instruction', 'Lets think step by step.'), ('few_shot_count', 5), ('generate_expert_identity', True), ('generate_intent_keywords', False), ('generate_reasoning', True), ('max_eval_batches', 6), ('min_correct_count', 3), ('mutate_refine_iterations', 3), ('mutation_rounds', 2), ('num_train_examples', 20), ('prompt_technique_name', 'critique_n_refine'), ('questions_batch_size', 1), ('refine_instruction', True), ('refine_task_eg_iterations', 3), ('seen_set_size', 20), ('style_variation', 5), ('task_description', 'You are a mathematics expert. You will be given a mathematics problem which you need to solve'), ('top_n', 1), ('unique_model_id', 'Qwen3-32B')]
Mutation
对初始化 Prompt 进行变异,也是通过LLM,也需要 Prompt,这里被称为 meta prompt,模板如下:
You are given a task description and a prompt instruction and different styles known as meta prompts:
[Task Description]: {task_description}
[Meta Prompt]: {meta_prompts}
Now you need to generate {num_variations} variations of following Instruction adaptively mixing meta prompt while keeping similar semantic meaning.
Make sure to wrap each generated prompt with <START> and <END>
[Prompt Instruction]: {prompt_instruction}
[Generated Prompts]:
对占位符进行填充后即可输入 LLM:
You are given a task description and a prompt instruction and different styles known as meta prompts:
[Task Description]: You are a mathematics expert. You will be given a mathematics problem which you need to solve
[Meta Prompt]: How could I devise an experiment to help solve that problem?
Make a list of ideas for solving this problem, and apply them one by one to the problem to see if any progress can be made.
How could I measure progress on this problem?
How can I simplify the problem so that it is easier to solve?
What are the key assumptions underlying this problem?
Now you need to generate 5 variations of following Instruction adaptively mixing meta prompt while keeping similar semantic meaning.
Make sure to wrap each generated prompt with <START> and <END>
[Prompt Instruction]: Lets think step by step.
[Generated Prompts]:
LLM 输出:
<START>
Let's approach this problem by first brainstorming a list of potential strategies. For each strategy, we can test it on the problem to see if it leads to any meaningful progress. How can we measure whether we're making progress? Also, consider simplifying the problem to make it more manageable. What assumptions are we making about the problem?
<END>
<START>
To solve this problem, let's break it down into smaller parts. First, think about how we could design an experiment or test to explore the problem further. Then, consider different methods for solving it and apply them step by step. How can we track our progress? What simplifications might help? What are the key assumptions we're relying on?
<END>
<START>
Let's take a structured approach to solving this problem. Start by listing possible ideas or methods for solving it. Try each one in turn to see if it helps. How can we define progress? Can we simplify the problem to make it easier to understand? What are the underlying assumptions that might be influencing our approach?
<END>
<START>
To tackle this problem, let's first consider how we might design an experiment or test to explore it. Then, generate a list of possible solutions and apply them one at a time. How can we measure whether we're moving in the right direction? What simplifications can we make? What assumptions are we making about the problem?
<END>
<START>
Let's work through this problem step by step. First, think about different ways to approach it and test them out. How can we measure progress? Can we simplify the problem to make it more approachable? What are the key assumptions we're making? How might an experiment help us better understand the problem?
<END>
由上可见,LLM一次输出 5 个变异Prompt, 来 3 次,共 15 个变异 Prompt。(当然外层还有 mutate_refine_iterations=3,这对我们的介绍不重要,忽略)
Scoring
给每个变异 Prompt 打分,打分方法是从 training data (这里为 gsm8k)中随机选择一道题,即question answer 对,把 question 放进变异 Prompt,让大模型预测,预测结果再跟 answer 比对,相同则为正确。每个变异 Prompt 测三道题,计算准确率。
让LLM预测答案的 Prompt:
You are given a prompt instruction and the following {questions_batch_size} questions of the same task.
[Instruction]: {instruction}
[Question]: {questions}
{answer_format}
[Answers]:
- instruction:即变异 Prompt,如:Let’s work through this problem step by step. First, think about different ways to approach it and test them out. How can we measure progress? Can we simplify the problem to make it more approachable? What are the key assumptions we’re making? How might an experiment help us better understand the problem?
- questions_batch_size:这里为 1
- answer_format:这里示例为:For each question present the reasoning followed by the correct answer.
- questions:James writes a 3-page letter to 2 different friends twice a week. How many pages does he write a year?’, ‘answer’: ‘He writes each friend 32=«32=6»6 pages a week\nSo he writes 62=«62=12»12 pages every week\nThat means he writes 1252=«1252=624»624 pages a year\n#### 624
Selection
选择准确率最高的变异 Prompt(或instruction)。
Sorted top n prompts: [[" \nTo solve this problem, let's break it down into smaller parts. First, think about how we could design an experiment or test to explore the problem further. Then, consider different methods for solving it and apply them step by step. How can we track our progress? What simplifications might help? What are the key assumptions we're relying on? \n", 1.0, [{'question': 'Jasper will serve charcuterie at his dinner party. He buys 2 pounds of cheddar cheese for $10, a pound of cream cheese that cost half the price of the cheddar cheese, and a pack of cold cuts that cost twice the price of the cheddar cheese. How much does he spend on the ingredients?', 'answer': 'A pound of cream cheese cost $10 / 2 = $<<10/2=5>>5.\nA pack of cold cuts cost $10 x 2 = $<<10*2=20>>20.\nJasper spent $10 + $5 + $20 = $<<10+5+20=35>>35 on the ingredients.\n#### 35', 'final_answer': '35'}]]]
Critique & Refine
如果准确率一经足够高了,则再做下强化。
Prompt to get critique:
I'm trying to write a prompt for zero-shot instruction task that will help the most capable and suitable agent to solve the task.
My current prompt is:
[CURRENT PROMPT] "
To solve this problem, let's break it down into smaller parts. First, think about how we could design an experiment or test to explore the problem further. Then, consider different methods for solving it and apply them step by step. How can we track our progress? What simplifications might help? What are the key assumptions we're relying on?
"
Now this prompt got the following examples correct:
[CORRECT EXAMPLES]
[Question] Jasper will serve charcuterie at his dinner party. He buys 2 pounds of cheddar cheese for $10, a pound of cream cheese that cost half the price of the cheddar cheese, and a pack of cold cuts that cost twice the price of the cheddar cheese. How much does he spend on the ingredients?
[Answer] A pound of cream cheese cost $10 / 2 = $<<10/2=5>>5.
A pack of cold cuts cost $10 x 2 = $<<10*2=20>>20.
Jasper spent $10 + $5 + $20 = $<<10+5+20=35>>35 on the ingredients.
#### 35
Since you cant use these examples, analyse and understand characteristics/complexity and diversity of these examples and their reasoning chain and
accordingly provide suggestions to further improve the prompt and make it better as a zero shot instruction task.
critique received from LLM:
Your current prompt is a strong starting point for a **zero-shot instruction task**, as it encourages **structured reasoning**, **problem decomposition**, and **critical thinking**. However, to make it even more effective for a wide range of tasks (especially math, logic, and real-world reasoning), we can refine it to be more **explicit**, **action-oriented**, and **aligned with the reasoning patterns** seen in the correct example.
---
### ✅ **Analysis of the Correct Example**
Let’s break down the correct example to understand what reasoning patterns are being used:
#### **Problem Type:**
- **Arithmetic word problem** involving:
- Unit pricing
- Multiplication/division
- Summation
- **Real-world context** (grocery shopping)
#### **Reasoning Chain:**
1. **Understand the relationships** between prices (e.g., "half the price of cheddar", "twice the price of cheddar").
2. **Calculate individual prices** using arithmetic.
3. **Sum the total** to get the final cost.
4. **Use a clear, step-by-step format** with intermediate calculations and final answer.
#### **Key Skills Demonstrated:**
- **Mathematical reasoning**
- **Attention to units and context**
- **Sequential problem-solving**
- **Clarity in intermediate steps**
---
### ✅ **Characteristics of a Good Zero-Shot Prompt for This Type of Task**
1. **Clarity and specificity** in what the model should do.
2. **Encouragement of step-by-step reasoning**.
3. **Explicit instructions** for tracking progress and justifying each step.
4. **Use of real-world context** to ground the reasoning.
5. **Flexibility** to handle a variety of problem types (not just math).
---
### ✅ **Improved Prompt (Enhanced for Zero-Shot Instruction)**
Here’s a revised version of your prompt that better supports the reasoning patterns seen in the correct example:
> **"To solve this problem, follow a clear, step-by-step process. First, identify the key information and relationships in the question. Then, break the problem into smaller parts and solve each part one at a time. Show your reasoning and calculations clearly. If applicable, use real-world context to guide your interpretation. Finally, combine your results to arrive at the final answer. Make sure to explain your steps and assumptions as you go."**
---
### ✅ **Why This Prompt is Better**
| Feature | Why It Helps |
|--------|--------------|
| **Step-by-step instruction** | Encourages structured reasoning, which is critical for math and logic problems. |
| **Identification of key info** | Helps the model focus on relevant data and avoid distractions. |
| **Use of real-world context** | Grounds abstract reasoning in practical understanding. |
| **Explanation of steps and assumptions** | Promotes transparency and traceability in the reasoning process. |
| **Flexibility** | Works for a wide range of problem types (math, logic, text-based reasoning). |
---
### ✅ **Optional Additions (for More Advanced Tasks)**
If you're targeting more complex or abstract tasks, you can optionally add:
> **"If the problem involves multiple possible approaches, consider each one and explain why you choose the best one. If you're unsure about a step, explain your uncertainty and how you might resolve it."**
This helps the model handle ambiguity and uncertainty, which is important in real-world problem-solving.
---
### ✅ **Final Suggestion**
Use the improved prompt as a **baseline**, and consider tailoring it slightly depending on the **type of task** (e.g., math, logic, text comprehension). For example:
- **For math problems:** Emphasize calculations and unit tracking.
- **For logic problems:** Emphasize assumptions and rule-based reasoning.
- **For text comprehension:** Emphasize identifying key details and drawing inferences.
---
Let me know if you'd like a version of the prompt tailored to a specific domain (e.g., math, science, coding, etc.)!
Prompt to get Refinement after critique, from LLM:
I'm trying to write a zero-shot instruction that will help the most capable and suitable agent to solve the task.
My current prompt is: "
To solve this problem, let's break it down into smaller parts. First, think about how we could design an experiment or test to explore the problem further. Then, consider different methods for solving it and apply them step by step. How can we track our progress? What simplifications might help? What are the key assumptions we're relying on?
"
But this prompt gets the following examples wrong:
[Question] Jasper will serve charcuterie at his dinner party. He buys 2 pounds of cheddar cheese for $10, a pound of cream cheese that cost half the price of the cheddar cheese, and a pack of cold cuts that cost twice the price of the cheddar cheese. How much does he spend on the ingredients?
[Answer] A pound of cream cheese cost $10 / 2 = $<<10/2=5>>5.
A pack of cold cuts cost $10 x 2 = $<<10*2=20>>20.
Jasper spent $10 + $5 + $20 = $<<10+5+20=35>>35 on the ingredients.
#### 35
On carefully analysing these examples, following are the critiques related to prompt Your current prompt is a strong starting point for a **zero-shot instruction task**, as it encourages **structured reasoning**, **problem decomposition**, and **critical thinking**. However, to make it even more effective for a wide range of tasks (especially math, logic, and real-world reasoning), we can refine it to be more **explicit**, **action-oriented**, and **aligned with the reasoning patterns** seen in the correct example.
---
### ✅ **Analysis of the Correct Example**
Let’s break down the correct example to understand what reasoning patterns are being used:
#### **Problem Type:**
- **Arithmetic word problem** involving:
- Unit pricing
- Multiplication/division
- Summation
- **Real-world context** (grocery shopping)
#### **Reasoning Chain:**
1. **Understand the relationships** between prices (e.g., "half the price of cheddar", "twice the price of cheddar").
2. **Calculate individual prices** using arithmetic.
3. **Sum the total** to get the final cost.
4. **Use a clear, step-by-step format** with intermediate calculations and final answer.
#### **Key Skills Demonstrated:**
- **Mathematical reasoning**
- **Attention to units and context**
- **Sequential problem-solving**
- **Clarity in intermediate steps**
---
### ✅ **Characteristics of a Good Zero-Shot Prompt for This Type of Task**
1. **Clarity and specificity** in what the model should do.
2. **Encouragement of step-by-step reasoning**.
3. **Explicit instructions** for tracking progress and justifying each step.
4. **Use of real-world context** to ground the reasoning.
5. **Flexibility** to handle a variety of problem types (not just math).
---
### ✅ **Improved Prompt (Enhanced for Zero-Shot Instruction)**
Here’s a revised version of your prompt that better supports the reasoning patterns seen in the correct example:
> **"To solve this problem, follow a clear, step-by-step process. First, identify the key information and relationships in the question. Then, break the problem into smaller parts and solve each part one at a time. Show your reasoning and calculations clearly. If applicable, use real-world context to guide your interpretation. Finally, combine your results to arrive at the final answer. Make sure to explain your steps and assumptions as you go."**
---
### ✅ **Why This Prompt is Better**
| Feature | Why It Helps |
|--------|--------------|
| **Step-by-step instruction** | Encourages structured reasoning, which is critical for math and logic problems. |
| **Identification of key info** | Helps the model focus on relevant data and avoid distractions. |
| **Use of real-world context** | Grounds abstract reasoning in practical understanding. |
| **Explanation of steps and assumptions** | Promotes transparency and traceability in the reasoning process. |
| **Flexibility** | Works for a wide range of problem types (math, logic, text-based reasoning). |
---
### ✅ **Optional Additions (for More Advanced Tasks)**
If you're targeting more complex or abstract tasks, you can optionally add:
> **"If the problem involves multiple possible approaches, consider each one and explain why you choose the best one. If you're unsure about a step, explain your uncertainty and how you might resolve it."**
This helps the model handle ambiguity and uncertainty, which is important in real-world problem-solving.
---
### ✅ **Final Suggestion**
Use the improved prompt as a **baseline**, and consider tailoring it slightly depending on the **type of task** (e.g., math, logic, text comprehension). For example:
- **For math problems:** Emphasize calculations and unit tracking.
- **For logic problems:** Emphasize assumptions and rule-based reasoning.
- **For text comprehension:** Emphasize identifying key details and drawing inferences.
---
Let me know if you'd like a version of the prompt tailored to a specific domain (e.g., math, science, coding, etc.)!
Use the critique smartly, refine the current prompt to make sure we dont get these examples wrong.
Based on the above information, Now I want you to write 1 different improved prompts.
Each prompt should be wrapped with <START> and <END>.
[Refined Prompts]:
Refined prompts received from LLM:
To solve this problem, begin by identifying the key numbers, relationships, and context in the question. Break the problem into smaller, manageable parts and solve each part step by step. Clearly show your calculations and reasoning for each step. Use the real-world context to guide your interpretation where necessary. Finally, combine your results to determine the final answer. Make sure to explain your process and any assumptions you make along the way.
得到 refined_prompts:
[' \nTo solve this problem, begin by identifying the key numbers, relationships, and context in the question. Break the problem into smaller, manageable parts and solve each part step by step. Clearly show your calculations and reasoning for each step. Use the real-world context to guide your interpretation where necessary. Finally, combine your results to determine the final answer. Make sure to explain your process and any assumptions you make along the way. \n']
重复打分:
rompt_score_list [[' \nTo solve this problem, begin by identifying the key numbers, relationships, and context in the question. Break the problem into smaller, manageable parts and solve each part step by step. Clearly show your calculations and reasoning for each step. Use the real-world context to guide your interpretation where necessary. Finally, combine your results to determine the final answer. Make sure to explain your process and any assumptions you make along the way. \n', 0.5, [{'question': 'Joy can read 8 pages of a book in 20 minutes. How many hours will it take her to read 120 pages?', 'answer': 'In one hour, there are 3 sets of 20 minutes.\nSo, Joy can read 8 x 3 = <<8*3=24>>24 pages in an hour.\nIt will take her 120/24 = <<120/24=5>>5 hours to read 120 pages.\n#### 5', 'final_answer': '5'}]]]
Sorted top n prompts:
[[" \nTo solve this problem, let's break it down into smaller parts. First, think about how we could design an experiment or test to explore the problem further. Then, consider different methods for solving it and apply them step by step. How can we track our progress? What simplifications might help? What are the key assumptions we're relying on? \n", 1.0, [{'question': 'Jasper will serve charcuterie at his dinner party. He buys 2 pounds of cheddar cheese for $10, a pound of cream cheese that cost half the price of the cheddar cheese, and a pack of cold cuts that cost twice the price of the cheddar cheese. How much does he spend on the ingredients?', 'answer': 'A pound of cream cheese cost $10 / 2 = $<<10/2=5>>5.\nA pack of cold cuts cost $10 x 2 = $<<10*2=20>>20.\nJasper spent $10 + $5 + $20 = $<<10+5+20=35>>35 on the ingredients.\n#### 35', 'final_answer': '35'}]]]
生成的最优 prompt 赋值给 base_instruction。
生成 final_prompt 之前,加上之前预测错误的问答作为 few shot示例,并在示例中加上推理。
final_prompt: |
{instruction}
{few_shot_examples}
{answer_format}
加推理的 Prompt 如下:
generate_reason_template: |
You are given a task description and instruction followed by a set of correct examples of the task.
[Task Description]: {task_description}
[Instruction]: {instruction}
Each example has a question denoted by question [Question] and a final answer [Answer] .
[Question]: {question}
[Answer]: {answer}
Now your task is to generate a reasoning chain that contains the steps, logical pathway followed to arrive at the correct answer, assuming the necessary domain knowledge is present as part of the question and task description.
Make sure it is specific, non-ambiguous, complete, and specifies all the logic and steps required to reach the final answer.
[Improved Reasoning Chain]:
其它步骤略。
Final best prompt:
You are a mathematics expert. You will be given a mathematics problem which you need to solve. To approach this, first consider how you might create an experiment or test to better understand the problem. Then, generate a list of possible solution strategies and try applying them one at a time. Think about how you can measure your progress, and whether simplifying the problem could make it more manageable. Also, identify the key assumptions that underpin the problem.
[Question] A rectangular prism has a length of 10 cm, a width of 5 cm, and a height of 4 cm. If the prism is filled with water, how many liters of water can it hold? (1 cm³ = 1 mL)
[Answer] To determine how many liters of water a rectangular prism can hold, we need to follow a step-by-step reasoning process based on the given dimensions and the conversion between cubic centimeters and milliliters.
1. **Understand the shape and its volume formula**:
A rectangular prism is a 3D shape with length (l), width (w), and height (h). The volume $ V $ of a rectangular prism is calculated using the formula:
$$
V = l \times w \times h
$$
2. **Substitute the given dimensions into the formula**:
The prism has a length of 10 cm, a width of 5 cm, and a height of 4 cm. Substituting these values:
$$
V = 10 \, \text{cm} \times 5 \, \text{cm} \times 4 \, \text{cm}
$$
3. **Calculate the volume in cubic centimeters**:
$$
V = 200 \, \text{cm}^3
$$
4. **Convert cubic centimeters to milliliters**:
It is given that $ 1 \, \text{cm}^3 = 1 \, \text{mL} $, so:
$$
200 \, \text{cm}^3 = 200 \, \text{mL}
$$
5. **Convert milliliters to liters**:
Since $ 1 \, \text{L} = 1000 \, \text{mL} $, we divide the volume in milliliters by 1000:
$$
\frac{200 \, \text{mL}}{1000} = 0.2 \, \text{L}
$$
6. **Final Answer**:
The rectangular prism can hold **0.2 liters** of water. <ANS_START>0.2<ANS_END>
[Question] A bag contains 5 red marbles, 3 blue marbles, and 2 green marbles. If one marble is drawn at random and not replaced, what is the probability that the second marble drawn is not blue?
[Answer] To solve the problem, we need to determine the probability that the second marble drawn is **not blue**, given that the first marble is drawn at random and **not replaced**. The bag initially contains 5 red marbles, 3 blue marbles, and 2 green marbles, for a total of 10 marbles.
---
### Step 1: Understand the Problem and Identify Key Assumptions
- The marbles are drawn **without replacement**, meaning the first marble drawn affects the composition of the bag for the second draw.
- The first marble can be **red**, **blue**, or **green**.
- The second marble is to be **not blue**, i.e., it can be **red** or **green**.
- The total number of marbles decreases by 1 after the first draw.
- The probability of the second marble being not blue depends on the **outcome of the first draw**.
---
### Step 2: Break the Problem into Cases
We consider all possible outcomes for the first draw and calculate the probability of the second marble being not blue in each case. Then, we use the **law of total probability** to combine the results.
Let’s define the events:
- $ R_1 $: First marble is red
- $ B_1 $: First marble is blue
- $ G_1 $: First marble is green
- $ N_2 $: Second marble is not blue (i.e., red or green)
We want to compute $ P(N_2) $, the total probability that the second marble is not blue.
Using the law of total probability:
$$
P(N_2) = P(N_2 | R_1)P(R_1) + P(N_2 | B_1)P(B_1) + P(N_2 | G_1)P(G_1)
$$
---
### Step 3: Compute Individual Probabilities
#### 1. $ P(R_1) = \frac{5}{10} = \frac{1}{2} $
If the first marble is red, the remaining marbles are: 4 red, 3 blue, 2 green → 9 total.
- Number of non-blue marbles left: 4 red + 2 green = 6
- So, $ P(N_2 | R_1) = \frac{6}{9} = \frac{2}{3} $
#### 2. $ P(B_1) = \frac{3}{10} $
If the first marble is blue, the remaining marbles are: 5 red, 2 blue, 2 green → 9 total.
- Number of non-blue marbles left: 5 red + 2 green = 7
- So, $ P(N_2 | B_1) = \frac{7}{9} $
#### 3. $ P(G_1) = \frac{2}{10} = \frac{1}{5} $
If the first marble is green, the remaining marbles are: 5 red, 3 blue, 1 green → 9 total.
- Number of non-blue marbles left: 5 red + 1 green = 6
- So, $ P(N_2 | G_1) = \frac{6}{9} = \frac{2}{3} $
---
### Step 4: Apply the Law of Total Probability
Now plug in the values:
$$
P(N_2) = \left(\frac{2}{3} \cdot \frac{1}{2}\right) + \left(\frac{7}{9} \cdot \frac{3}{10}\right) + \left(\frac{2}{3} \cdot \frac{1}{5}\right)
$$
Compute each term:
- $ \frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3} $
- $ \frac{7}{9} \cdot \frac{3}{10} = \frac{21}{90} = \frac{7}{30} $
- $ \frac{2}{3} \cdot \frac{1}{5} = \frac{2}{15} $
Now sum the fractions:
$$
P(N_2) = \frac{1}{3} + \frac{7}{30} + \frac{2}{15}
$$
Convert all to a common denominator (30):
- $ \frac{1}{3} = \frac{10}{30} $
- $ \frac{7}{30} = \frac{7}{30} $
- $ \frac{2}{15} = \frac{4}{30} $
$$
P(N_2) = \frac{10 + 7 + 4}{30} = \frac{21}{30} = \frac{7}{10}
$$
---
### Final Answer:
$$
\boxed{\frac{7}{10}}
$$
This is the probability that the second marble drawn is **not blue**. <ANS_START>7<ANS_END>
[Question] A rectangle has a length that is 3 times its width. If the perimeter of the rectangle is 48 meters and the length and width must be whole numbers, what are the possible dimensions?
[Answer] To solve the problem, we are given the following:
- A rectangle has a length that is 3 times its width.
- The perimeter of the rectangle is 48 meters.
- The length and width must be whole numbers.
- We are to find the possible dimensions of the rectangle.
---
### Step 1: Define the variables
Let the width of the rectangle be $ w $ meters.
Since the length is 3 times the width, the length is $ 3w $ meters.
---
### Step 2: Use the formula for the perimeter of a rectangle
The perimeter $ P $ of a rectangle is given by:
$$
P = 2 \times (\text{length} + \text{width})
$$
Substitute the expressions for length and width:
$$
48 = 2 \times (3w + w)
$$
---
### Step 3: Simplify the equation
$$
48 = 2 \times (4w)
$$
$$
48 = 8w
$$
---
### Step 4: Solve for $ w $
$$
w = \frac{48}{8} = 6
$$
---
### Step 5: Find the length
Since the length is $ 3w $, we substitute $ w = 6 $:
$$
\text{Length} = 3 \times 6 = 18
$$
---
### Step 6: Verify the solution
Check the perimeter with the calculated dimensions:
$$
P = 2 \times (18 + 6) = 2 \times 24 = 48
$$
This matches the given perimeter, and both the length and width are whole numbers.
---
### Step 7: Determine the possible dimensions
The only possible dimensions that satisfy the given conditions are:
- Width = 6 meters
- Length = 18 meters
---
### Final Answer:
$$
\text{Width} = 6, \text{Length} = 18
$$
[Answer]: 6 <ANS_START>6<ANS_END>
[Question] A store offers a 15% discount on all items. If a customer buys a jacket that originally costs $80 and a pair of shoes that costs $60, and there is a 10% sales tax after the discount, what is the final price?
[Answer] To solve the problem, we need to calculate the final price a customer pays after applying a 15% discount and then adding a 10% sales tax. Here is the step-by-step reasoning chain:
1. **Understand the problem and identify the key components**:
- The store offers a 15% discount on all items.
- The customer buys a jacket for $80 and a pair of shoes for $60.
- After the discount, a 10% sales tax is applied to the total discounted price.
- The goal is to find the final price the customer pays.
2. **Calculate the total original price of the items**:
- Jacket: $80
- Shoes: $60
- Total original price = $80 + $60 = $140
3. **Apply the 15% discount to the total original price**:
- 15% of $140 = 0.15 × 140 = $21
- Discounted total = $140 - $21 = $119
4. **Apply the 10% sales tax to the discounted total**:
- 10% of $119 = 0.10 × 119 = $11.90
- Final price = $119 + $11.90 = $130.90
5. **Verify the calculations**:
- Total original price: $140
- Discount: $21
- Discounted total: $119
- Sales tax: $11.90
- Final price: $130.90
6. **Conclusion**:
- The final price the customer pays is $130.90.
This reasoning chain is specific, complete, and logically follows the steps required to solve the problem. <ANS_START>130.90<ANS_END>
[Question] A car travels at 60 mph for the first 100 miles and then slows down to 50 mph for the remaining 200 miles. How long will it take to travel the total 300 miles?
[Answer] To determine the total time it takes for the car to travel 300 miles, we can break the journey into two segments and calculate the time for each segment separately. Then, we sum the times to get the total time.
1. **First Segment:**
- Distance: 100 miles
- Speed: 60 mph
- Time = Distance / Speed = 100 / 60 = 1.6667 hours
2. **Second Segment:**
- Distance: 200 miles
- Speed: 50 mph
- Time = Distance / Speed = 200 / 50 = 4 hours
3. **Total Time:**
- Total Time = Time for First Segment + Time for Second Segment
- Total Time = 1.6667 + 4 = 5.6667 hours
4. **Rounding:**
- Rounding to two decimal places, the total time is 5.67 hours.
Thus, the car will take **5.67 hours** to travel the total 300 miles. <ANS_START>5.67<ANS_END>
For each question present the reasoning followed by the correct answer.
参考资料
- https://github.com/microsoft/PromptWizard