简介

车辆调度问题，英文是 Vehicle Routing Problem，简称 VRP，一般翻译成车辆路径问题。主要解决物流公司的痛点，怎么用最小成本把仓库的货物分发到各个站点。

本文先介绍 VRP 的问题定义和问题分析，然后是解法，包括精确解和近似解，最后介绍实现这些解法的相关工具。

问题定义

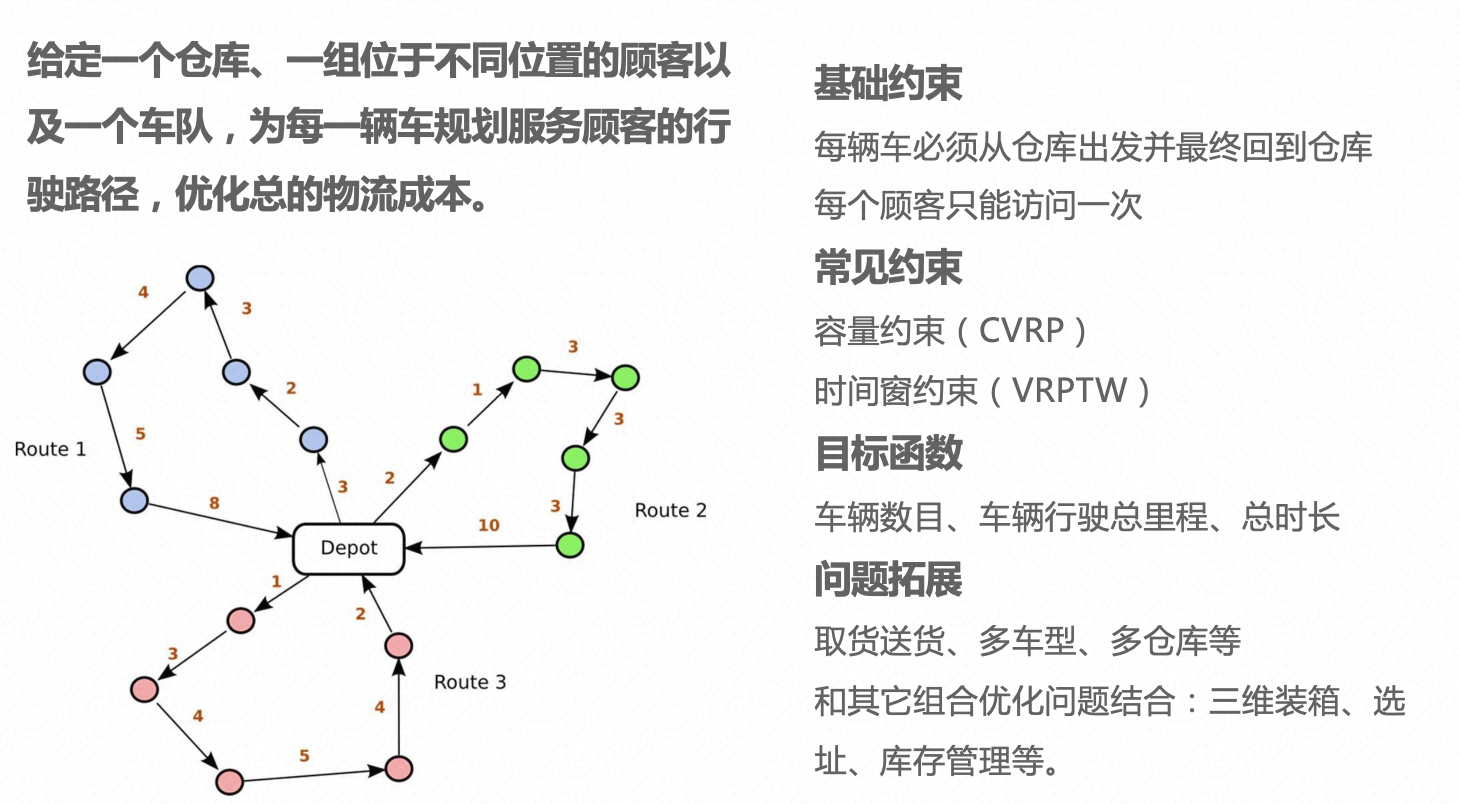
VRP 的定义，给定一个仓库，一组位于不同位置的顾客以及一个车队，要为每一辆车规划服务顾客的行驶路径，优化总的物流成本。即以最小的物流成本，把仓库中的物品分发给各个顾客。

VRP 一般模型的基础约束包括，每辆车必须从仓库出发并最终回到仓库，每个顾客只能访问一次，有且仅有一次。最常见的约束是容量约束和时间窗约束，容量约束是对车辆的运输能力进行限制，也是现在默认的 VRP，时间窗约束是对服务顾客的时间进行限制，即对每个顾客，车辆必须在其指定的时间段内到达，比如有些货需要赶飞机、赶火车，就必须在指定时间段到达，通常考虑硬时窗，即晚到不能进行服务，也有软时窗，也就是超时可以服务，但会导致总成本增加。

优化的目标有用车最少、车辆行驶总里程最少、耗时最少。一般公开数据集的评价标准是，先看用车数目，用车最少的得分最高，用车相同的情况下看行驶总里程，里程少的方案获胜。工程实现可根据具体需求来设计目标函数。

VRP 还有很多拓展，比如取货送货（顾客们有收发两种需求）、多车型、多仓库等等，还可以跟其它组合优化问题结合，如三维装箱、选址、库存管理等等。

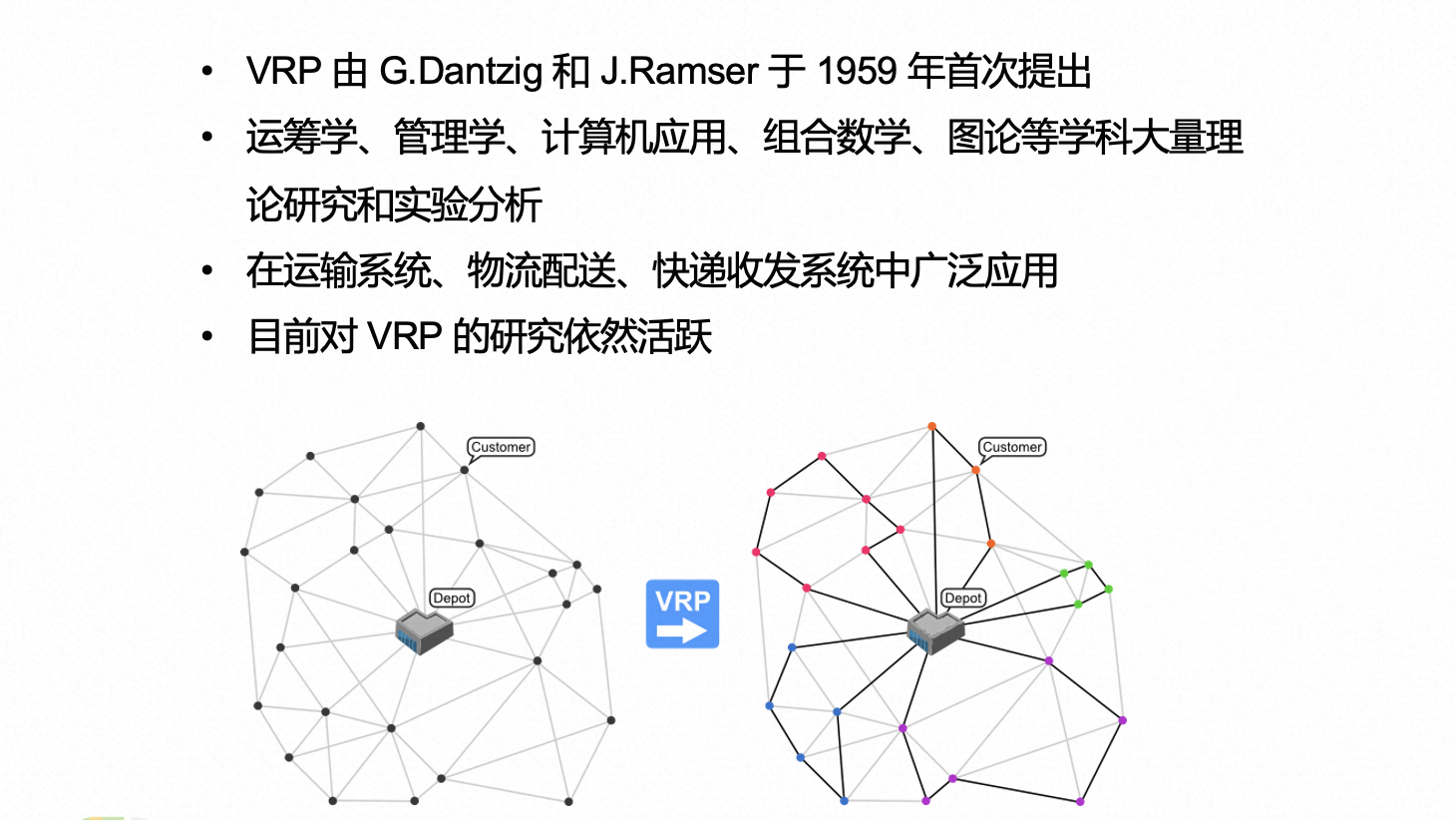
VRP 是 1959 年由 G.Dantzig 和 J.Ramser 两位数学家首次提出，很快就引起了运筹学、管理学、计算机应用、组合数学、图论等学科专家的高度重视，他们对此进行了大量理论研究和实验分析，取得了很大的研究进展，其研究成果在运输系统、物流配送系统、快递收发系统中已得到广泛应用，现在对 VRP 的研究仍然相当活跃。

其中丹齐格被称为线性规划之父，和冯诺依曼都是数学规划的创始人，运筹学中的单纯形法就是他发明的。

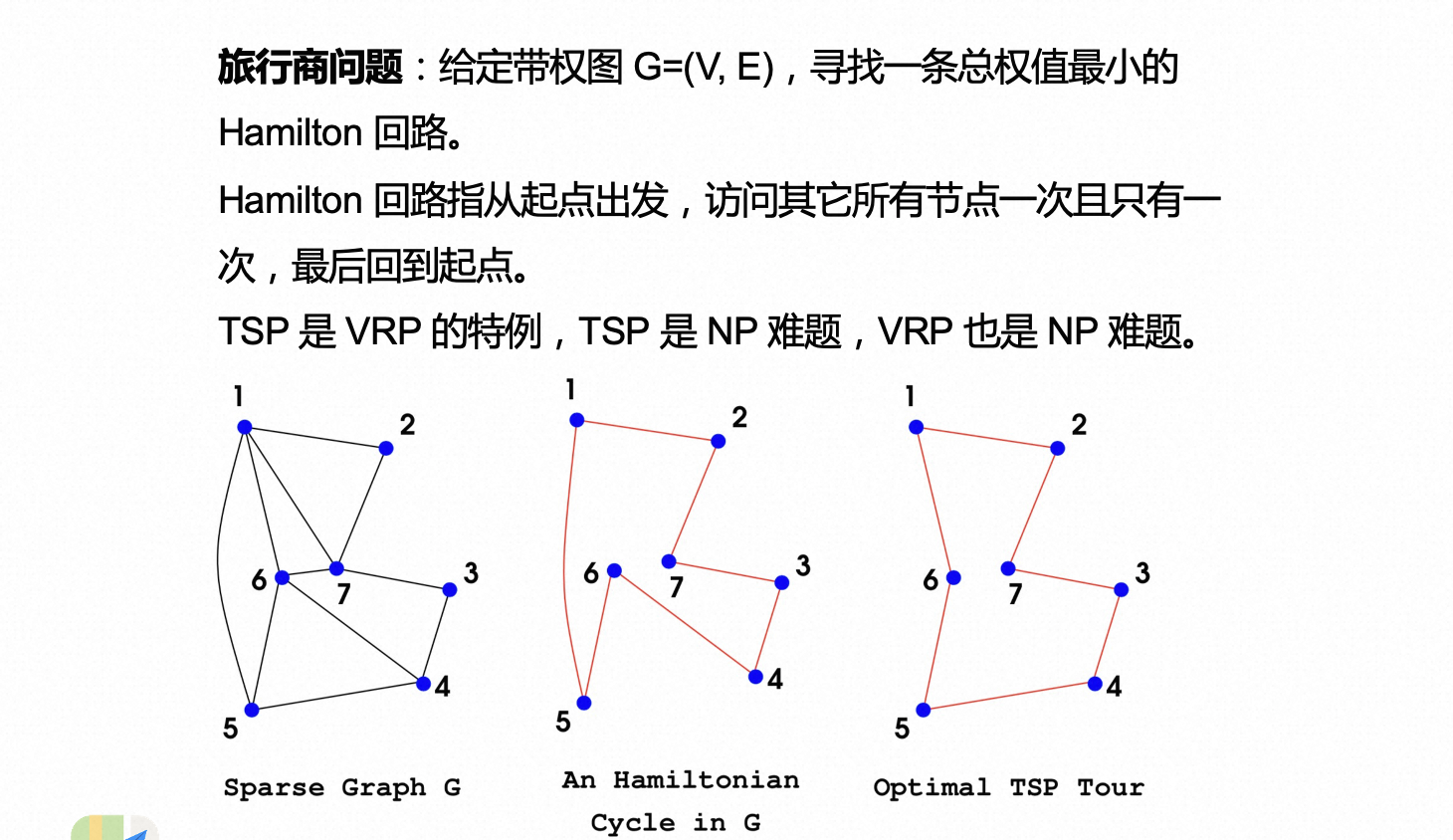
之前大家了解最多的应是旅行商问题，官方定义是，给定带权图 G=(V,E)，V 是顶点，E 是边，边带权重，求解一条最权值最小的哈密顿回路，哈密顿回路指从起点出发，访问其它所有节点一次且仅有后，再返回起点。可以说是给定一系列城市和每对城市之间的距离，求解访问每一个城市一次并回到起始城市的最短回路。

下面最左边是个稀疏图，并不是每两个顶点之间都有边相连，这里边是有权重的，只是没有标示；中间图是其中一个哈密顿回路，右图是最优的 TSP 路径。

由上图可知 TSP 其实是 VRP 的一个特例，一个最简单版的 VRP，没有容量、时间窗等的约束，任意一辆车都能装载所有货物然后运到所有网点。

所以在解 TSP 问题时，会相对简单，随意组合都是一个可行方案，虽然未必是最优。但 VRP 由于存在诸多约束，遍历组合搜索方案空间时，会遇到很多不可行的方案，难度自然大大增加。

TSP 是 NP 难题，VRP 自然也是。

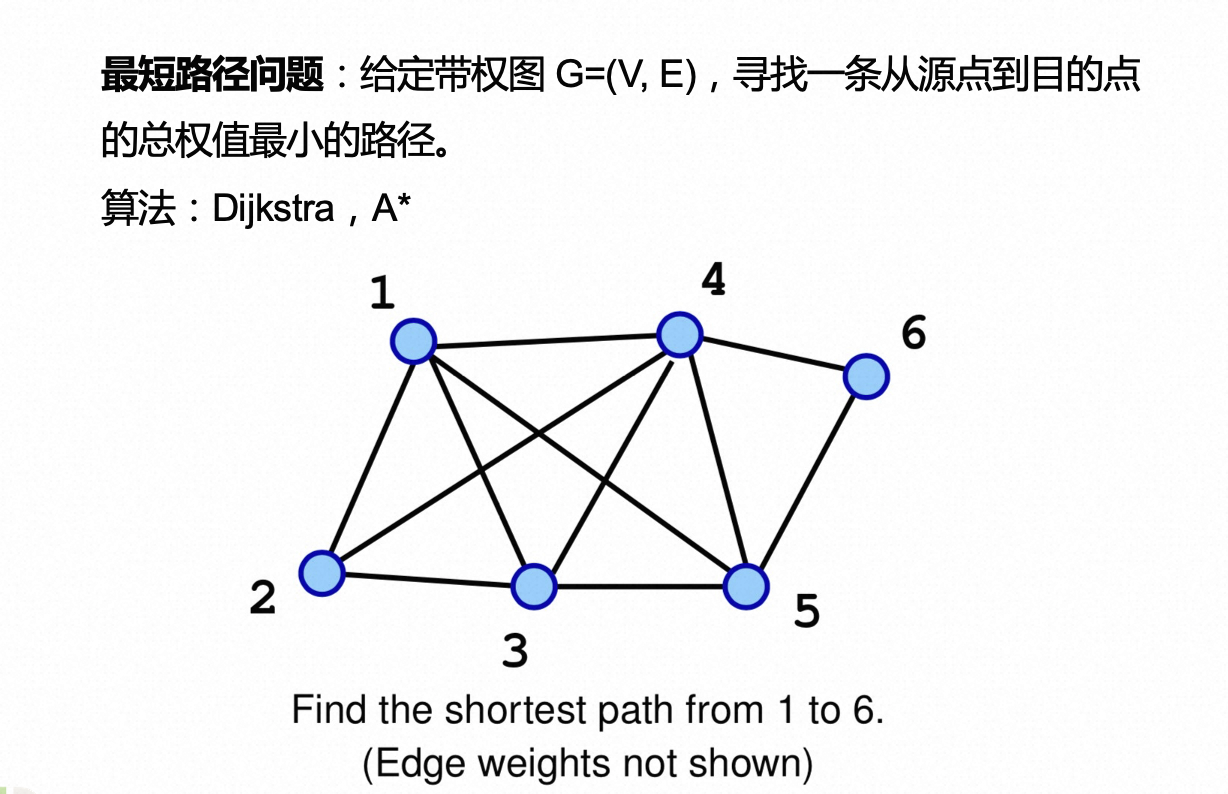
还有一个容易跟 VRP 混淆的是高德地图的路径规划，因为都是路径规划问题，但其实问题规模差别很大，高德地图的路径规划是单源路径规划，指的是在地图上寻找从源点到目的点的最短路径。没有要求必须经过所有点，更没有装载量、时间窗等约束，所以会相对简单的多，工程上也是毫秒级返回，都能得到最优解，大家用高德地图能感觉到，但 VRP 规模稍大点，分钟级的也可能只是满意解。

对于单源最短路径问题最常见的算法是 Dijkstra 和 A 星，当然还有其它的 Floyd、贝尔曼福特等，不再赘述，有兴趣可以查阅相关资料。

我们用的导航软件，从一地到另一地的最短路径问题，就是一个典型的运筹学问题。该问题目标是找到最短的驾驶路径 （或驾驶时间最短的路径），约束条件往往有单行路段以及每条路段的限速等等。

问题分析

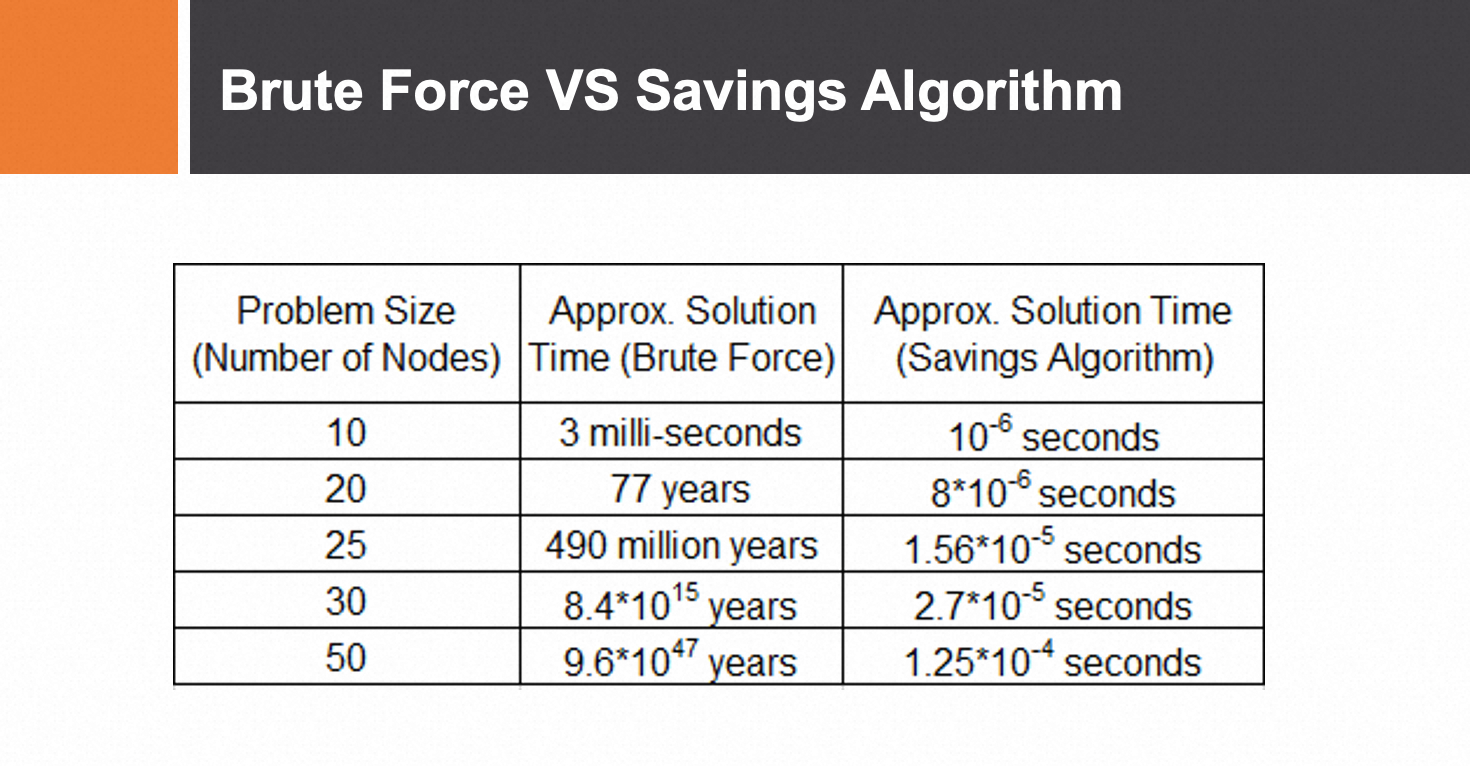
上图是有能力约束的车辆路径调度问题的数学模型。下面来感受下 VRP 暴力解的计算量。

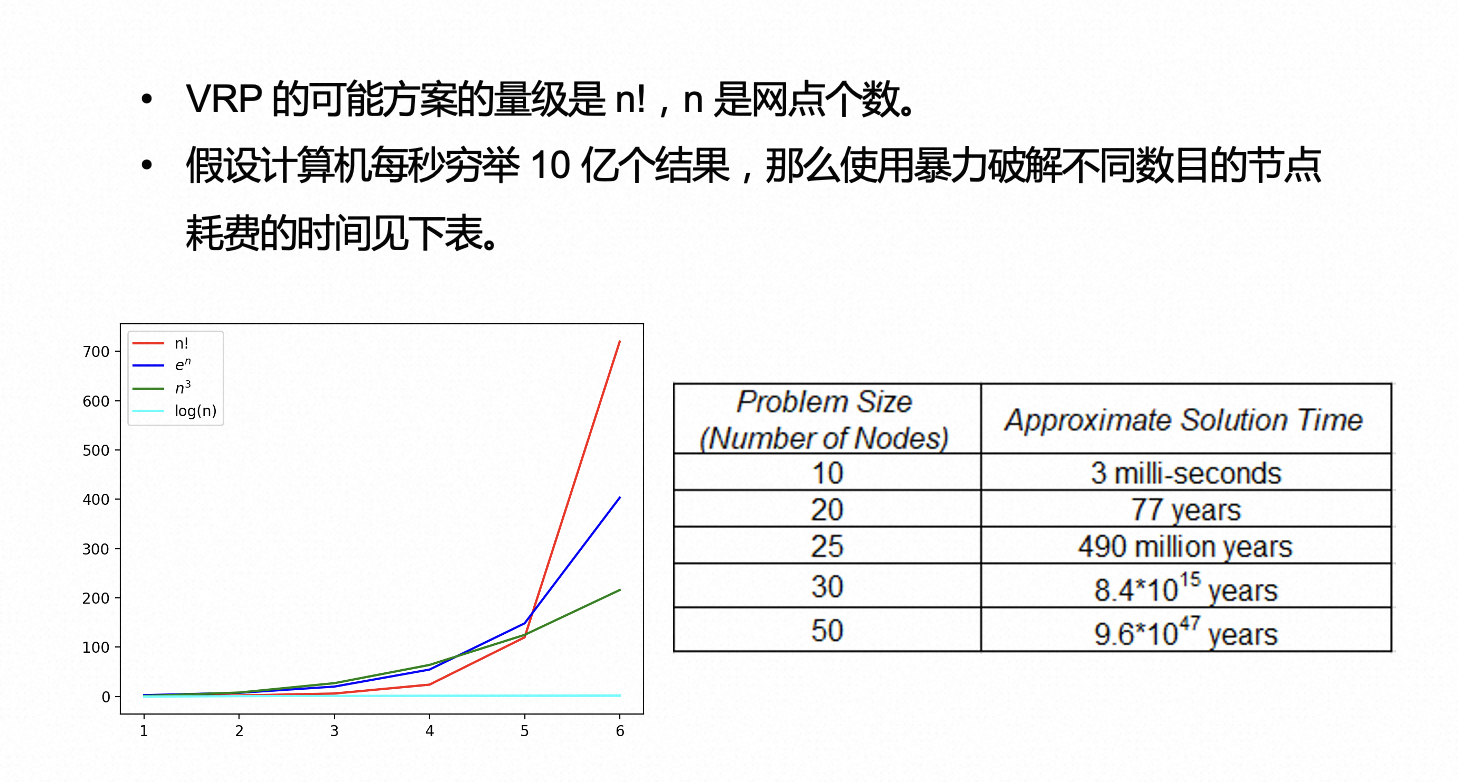
从穷举法的搜索空间来看，可以发现这个计算空间超级大，根本不可能通过增加机器来解决，再多的机器投进去也是炮灰，当然这个空间并不是完全没有秩序的，是有规律可循的，这是我们设计精确算法和启发式算法的原因，精确解其实还是探索了所有空间，只是有些空间还没搜索就发现没啥探索价值就放弃了，这就节省了很多宝贵的时间，但即使如此，当数据量大时，计算量依然极其庞大。所以才出现启发式算法，在大的空间内大量有效探索，但只能找到近似解，无法找到最优解。

算法篇

精确解

分支定界

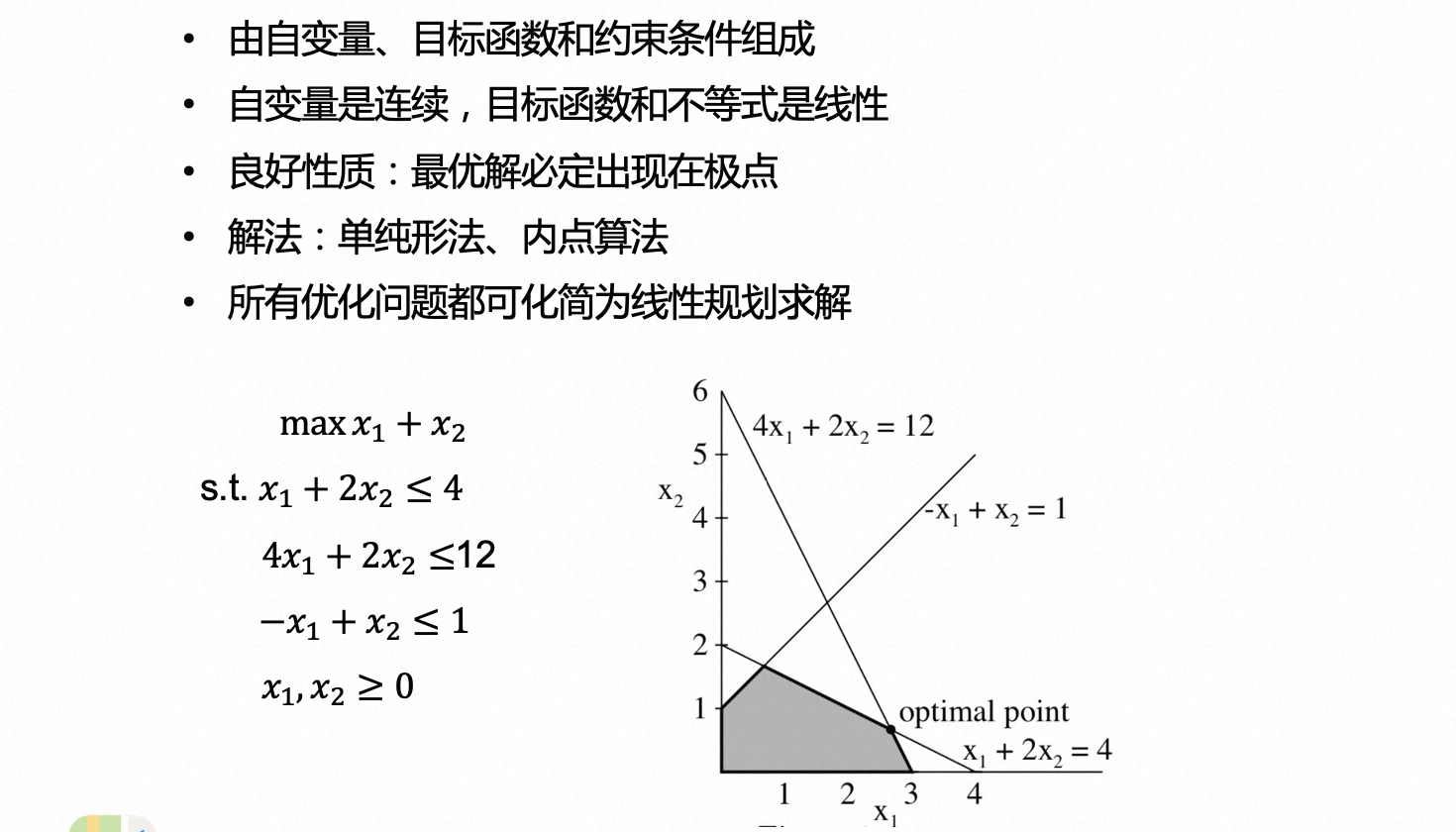
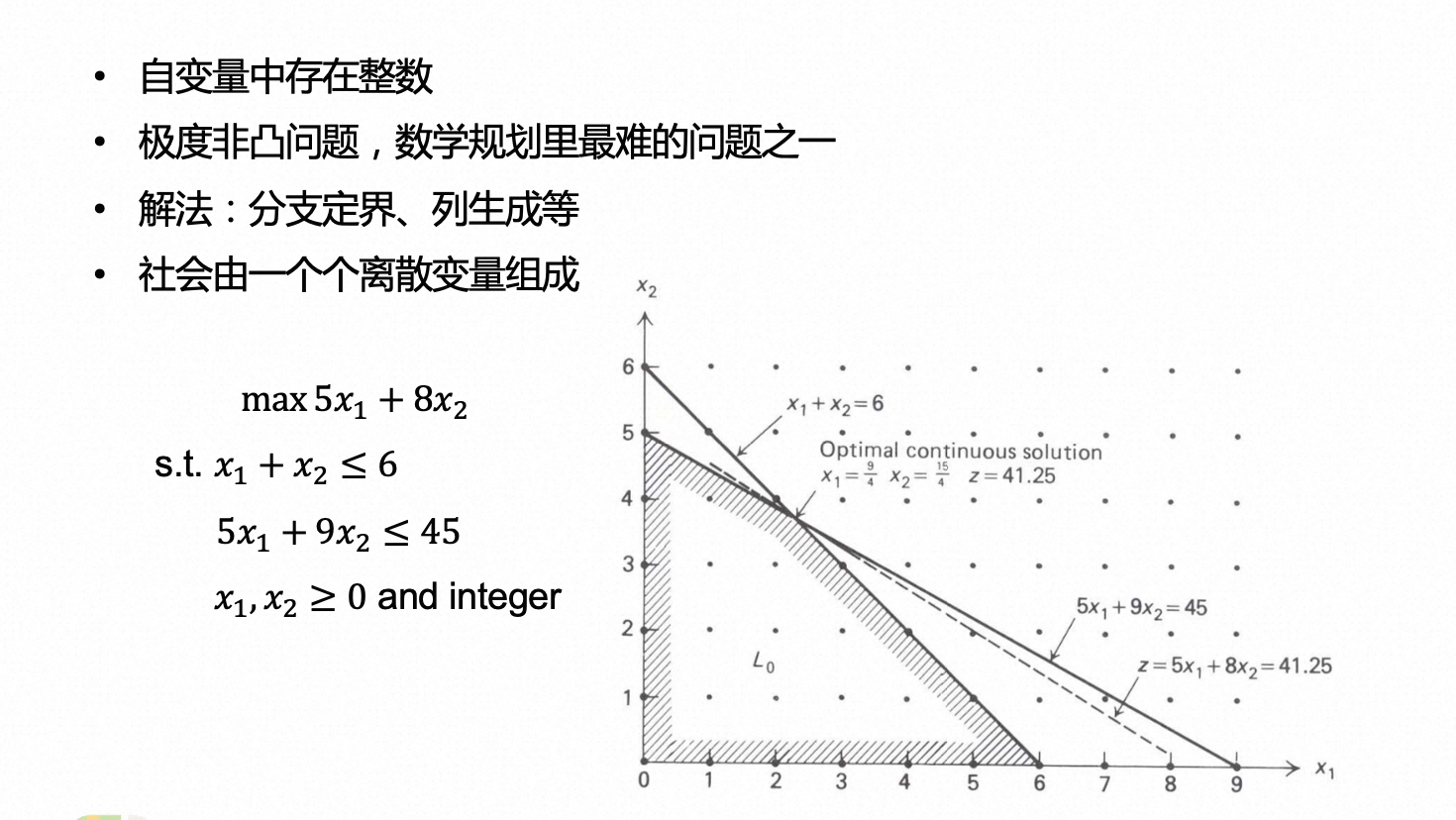
整数规划的精确算法通常需要用到分支定界法（Branch and Bound Method）,以及增加分支定界效率的各种技巧，例如割平面方法（Cutting Planes Method）。总的来说，求解整数规划的精确解是NP难的，也就是指数级算法复杂度（Exponential Time Solvable）。

整数规划问题被看作数学规划里、甚至是世界上最难的问题之一，被很多其他领域（例如机器学习）认为是不可追踪（Intractable）的问题，也就是他们直接放弃治疗了。

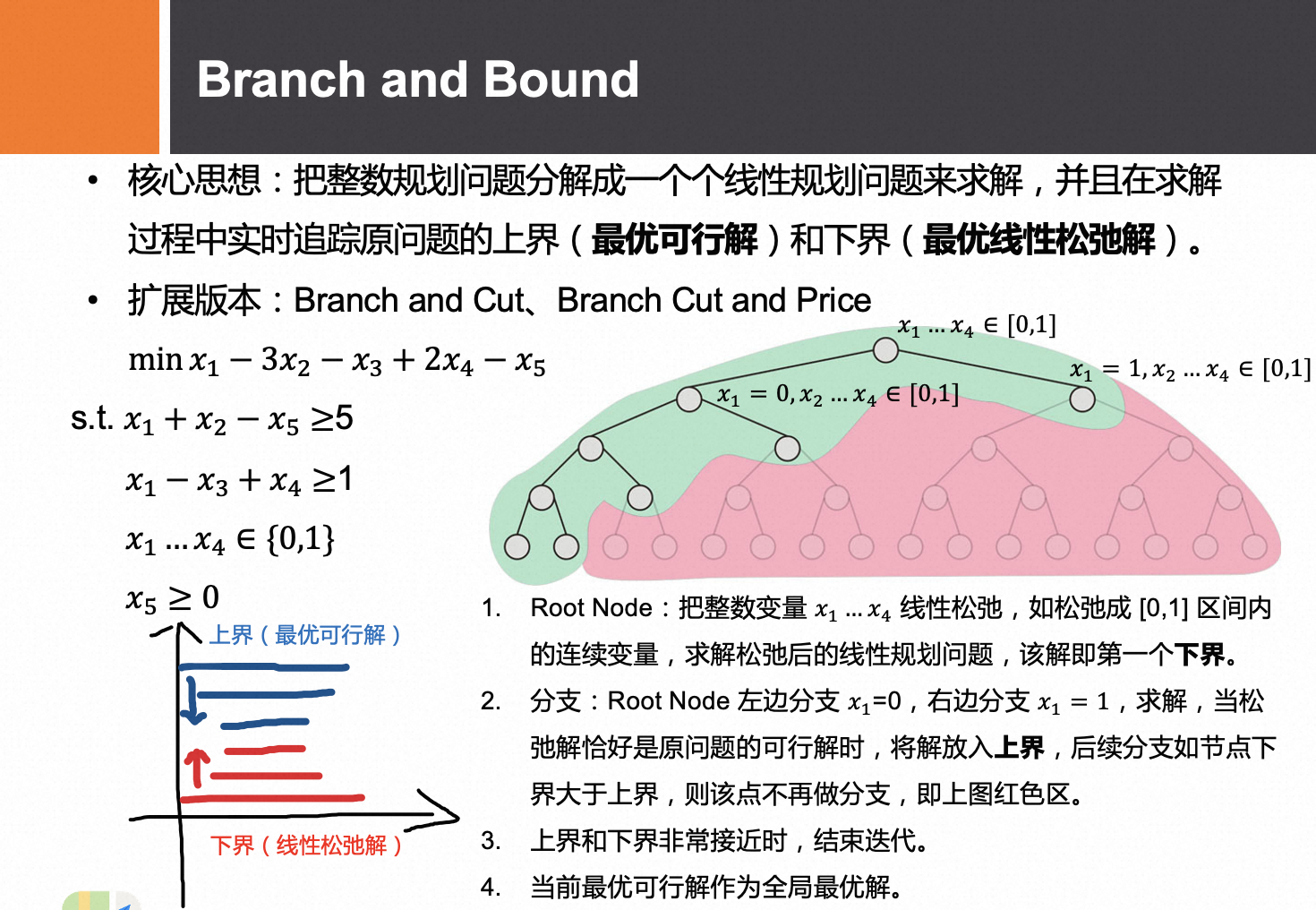
分枝界限法是由三栖学者查理德·卡普（Richard M.Karp）在20世纪60年代发明，成功求解含有65个城市的旅行商问题，创当时的记录。“分枝界限法”把问题的可行解展开如树的分枝，再经由各个分枝中寻找最佳解。

分枝界限法也能够使用在混合整数规划问题上，其为一种系统化的解法，以一般线性规划之单形法解得最佳解后，将非整数值之决策变量分割成为最接近的两个整数，分列条件，加入原问题中，形成两个子问题(或分枝)分别求解，如此便可求得目标函数值的上限（上界）或下限（下界），从其中寻得最佳解。

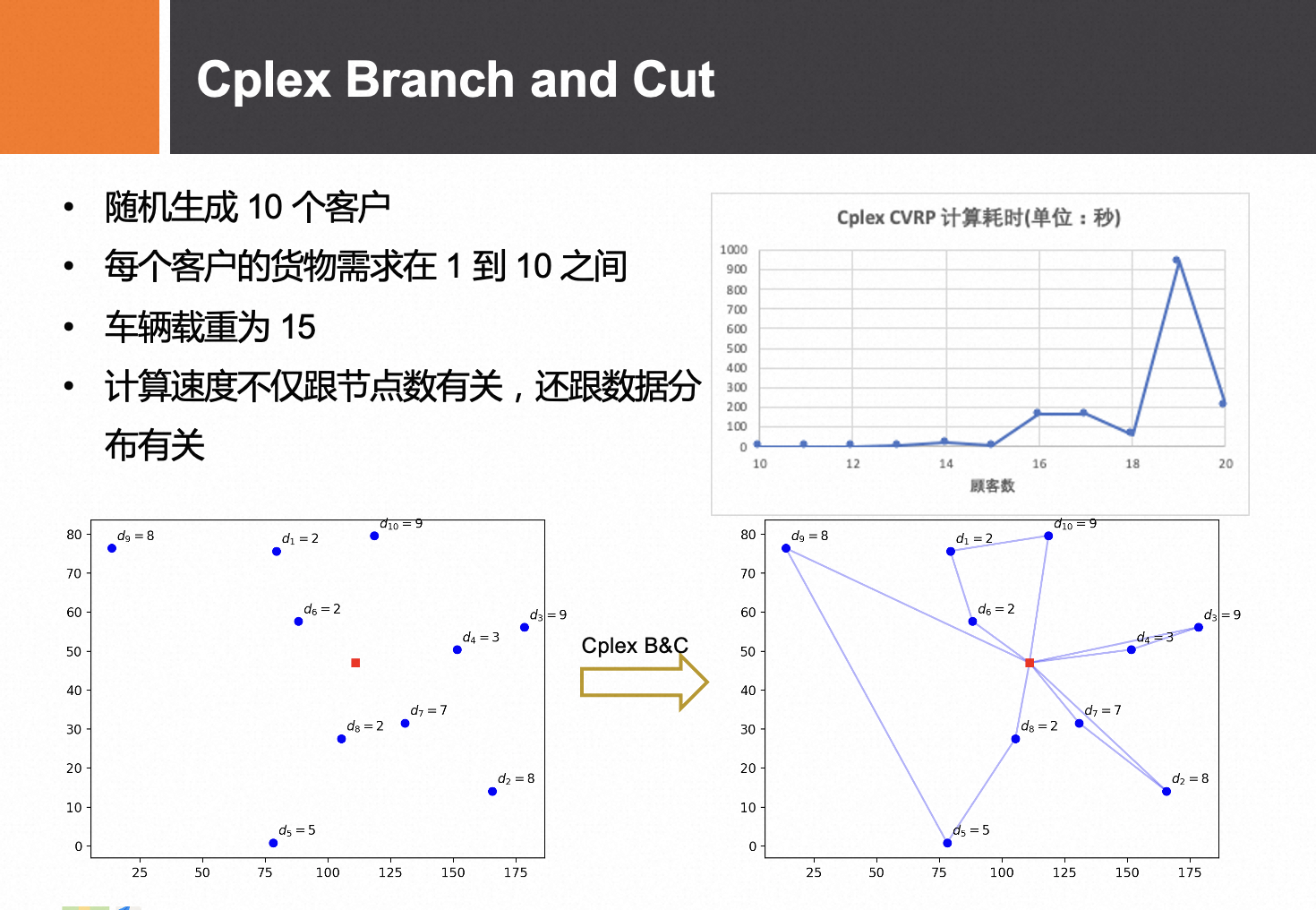
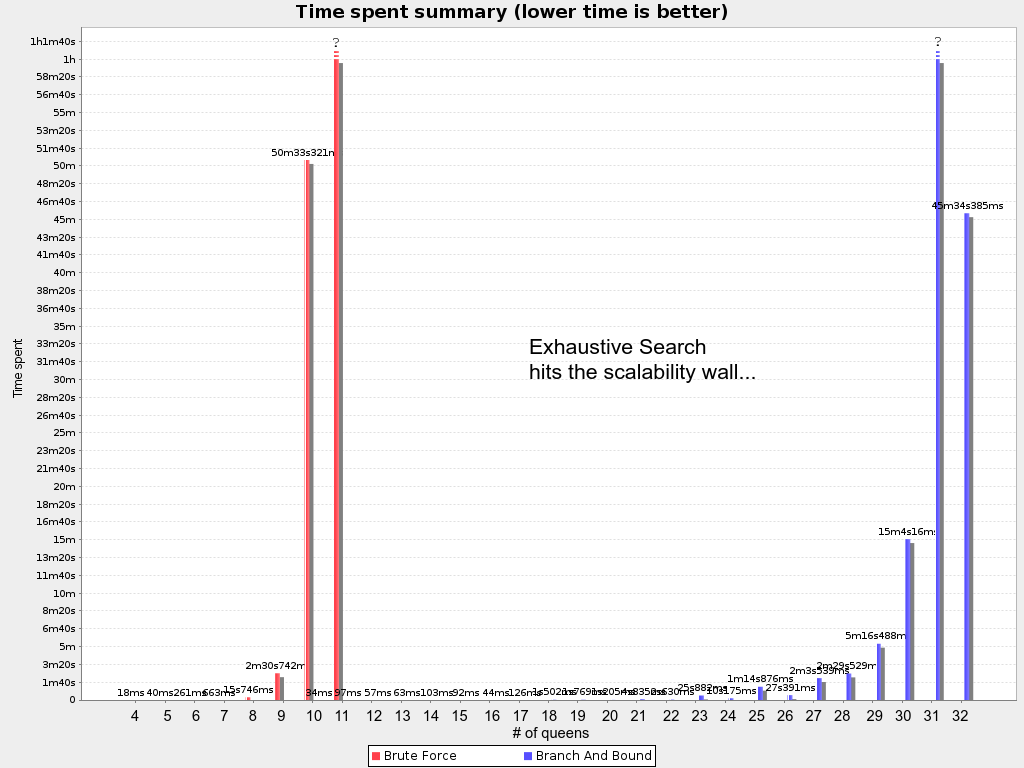
总的说来，精确性算法基于严格的数学手段，在可以求解的情况下，其解通常要优于人工智能算法。但由于引入严格的数学方法，计算量一般随问题规模的增大呈指数增长，因而无法避开指数爆炸问题，从而使该类算法只能有效求解中小规模的确定性VRP，并且通常这些算法都是针对某一特定问题设计的,适用能力较差,因此在实际中其应用范围很有限。

近似解

近似解的思想为通过一系列启发式的规则来构造和改变解，从而逐步提升解的质量。对于VRP而言，较为经典的启发式算法为Clarke-Wright算法等。此外，经过不断的探索研究，元启发式算法被证明在求解VRP方面具有很好的效果和效率。一些经过精心设计的元启发式算法，例如模拟退火、禁忌搜索、遗传算法、蚁群算法、变邻域搜索、自适应大规模邻域搜索算法等在求解VRP上有着非常好的表现。

节约法

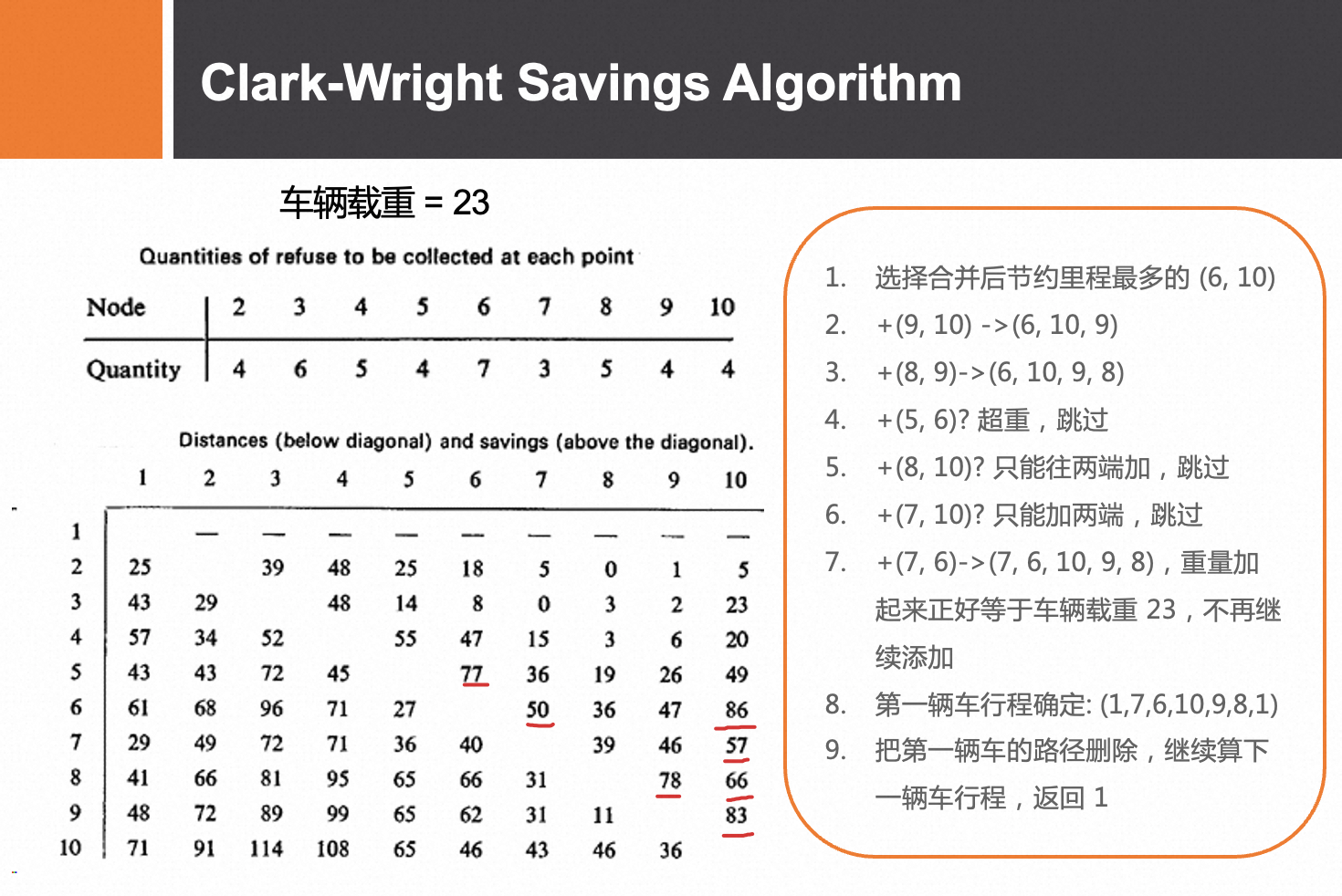
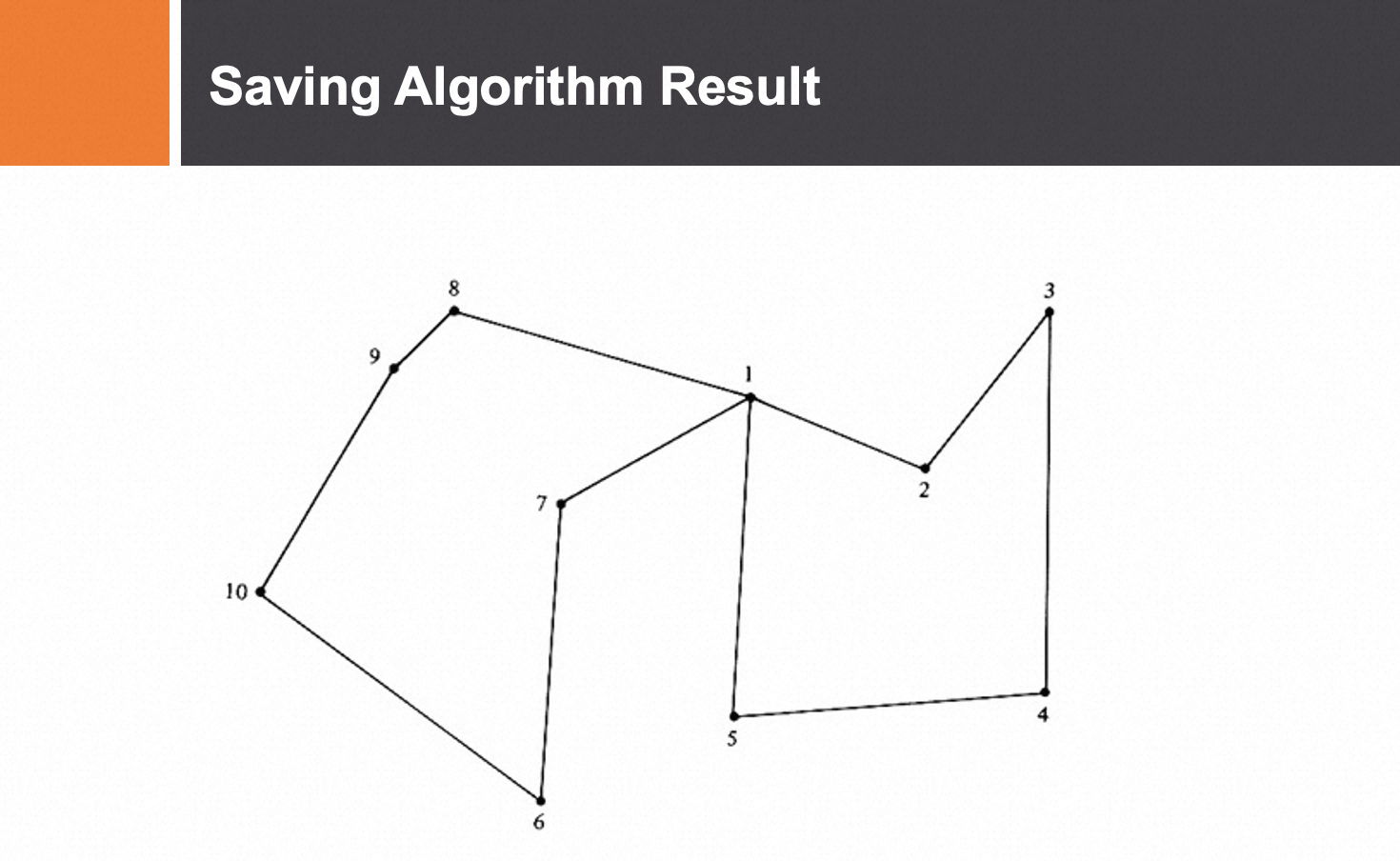
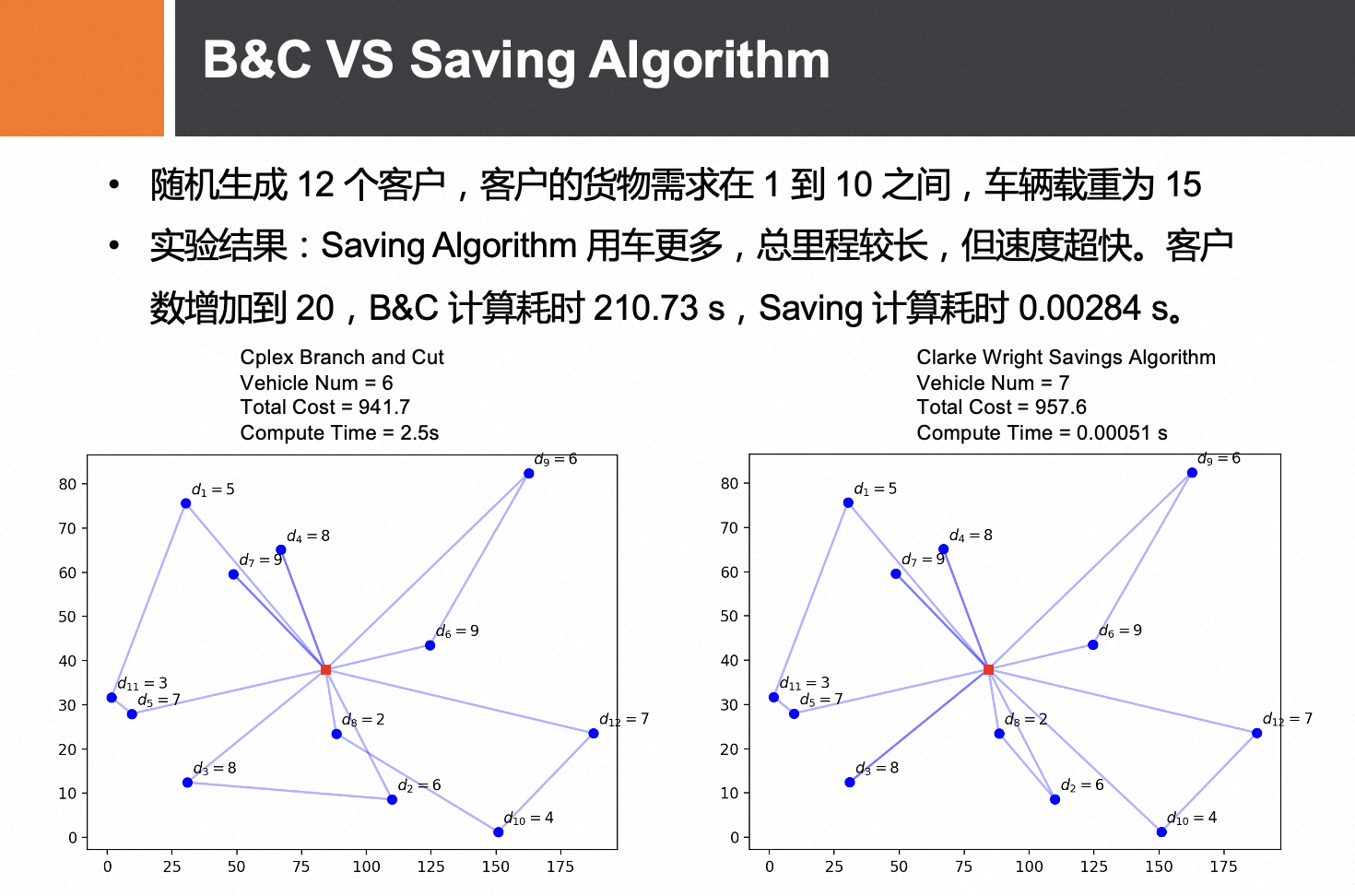
自适应大规模邻域搜索

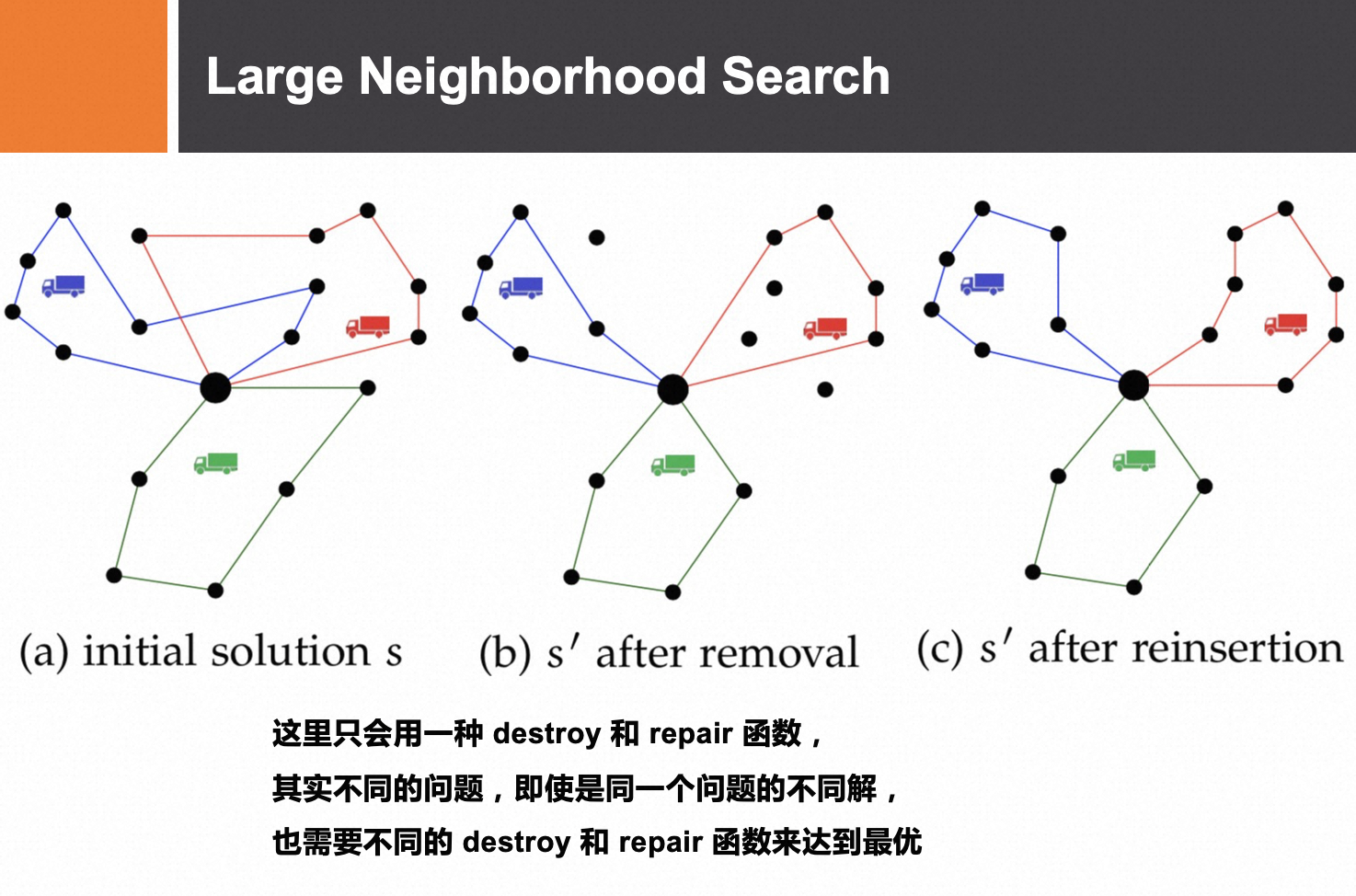
所谓邻域，简单说就是给定点附近其它点的集合。在距离空间中，邻域一般被定义给以给定圆点为圆心的一个圆。在组合优化问题中，邻域就是指对当前解进行一个操作（这个操作称为邻域动作）可以得到的所有解的集合。邻域的本质区别在于邻域动作的不同。

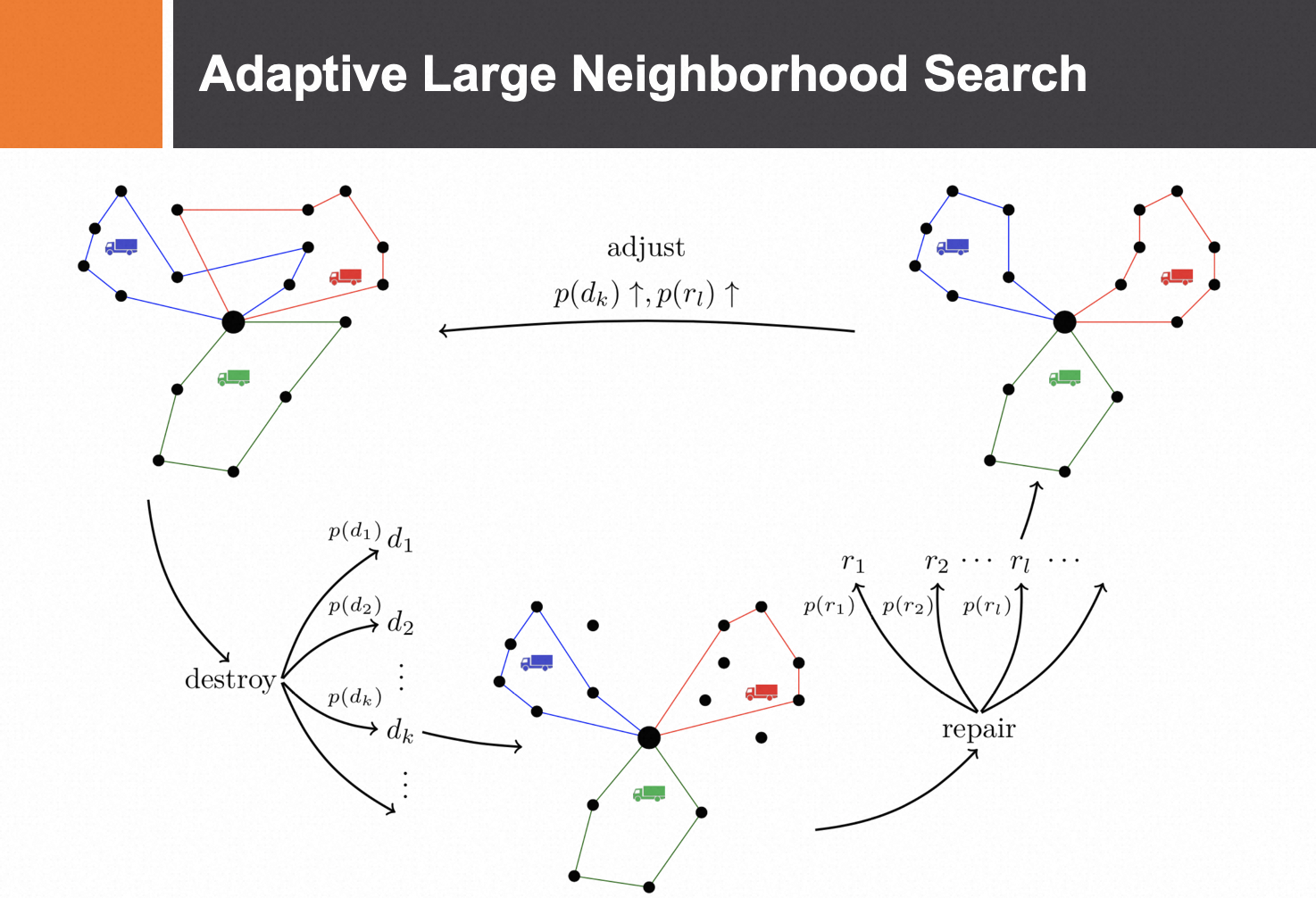
工具篇

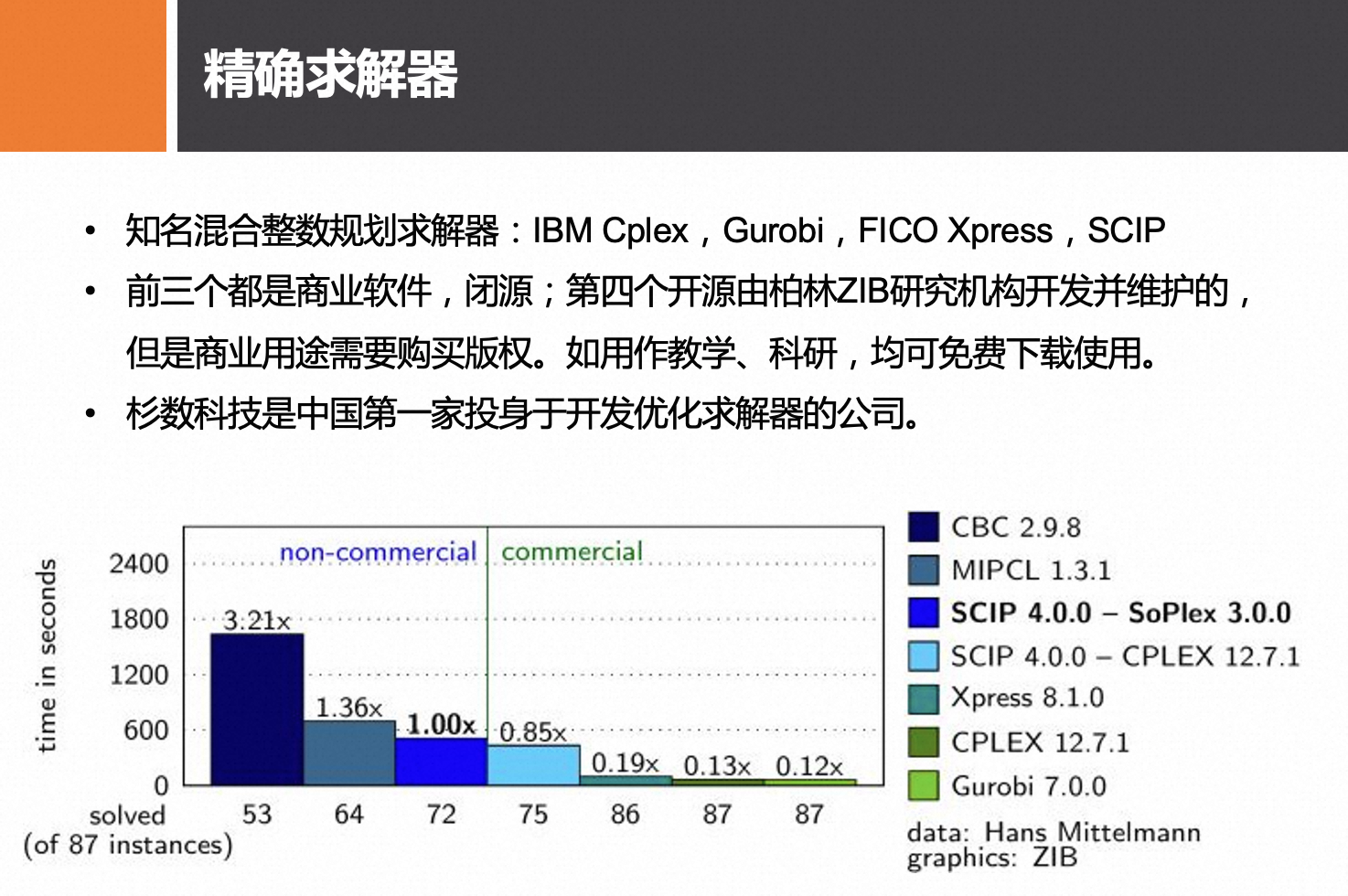
作为运筹学的引擎，优化求解器意义重大，因为所有混合整数规划模型的求解，都需要靠它。由于是NP难问题，求解的效率至关重要，不同求解器的求解速度也千差万别。例如同一个问题，用Cplex求解只需1分钟，用SCIP可能就需要1小时，你自己写B&B算法的程序，可能需要1天！（上图是各求解器效率对比）

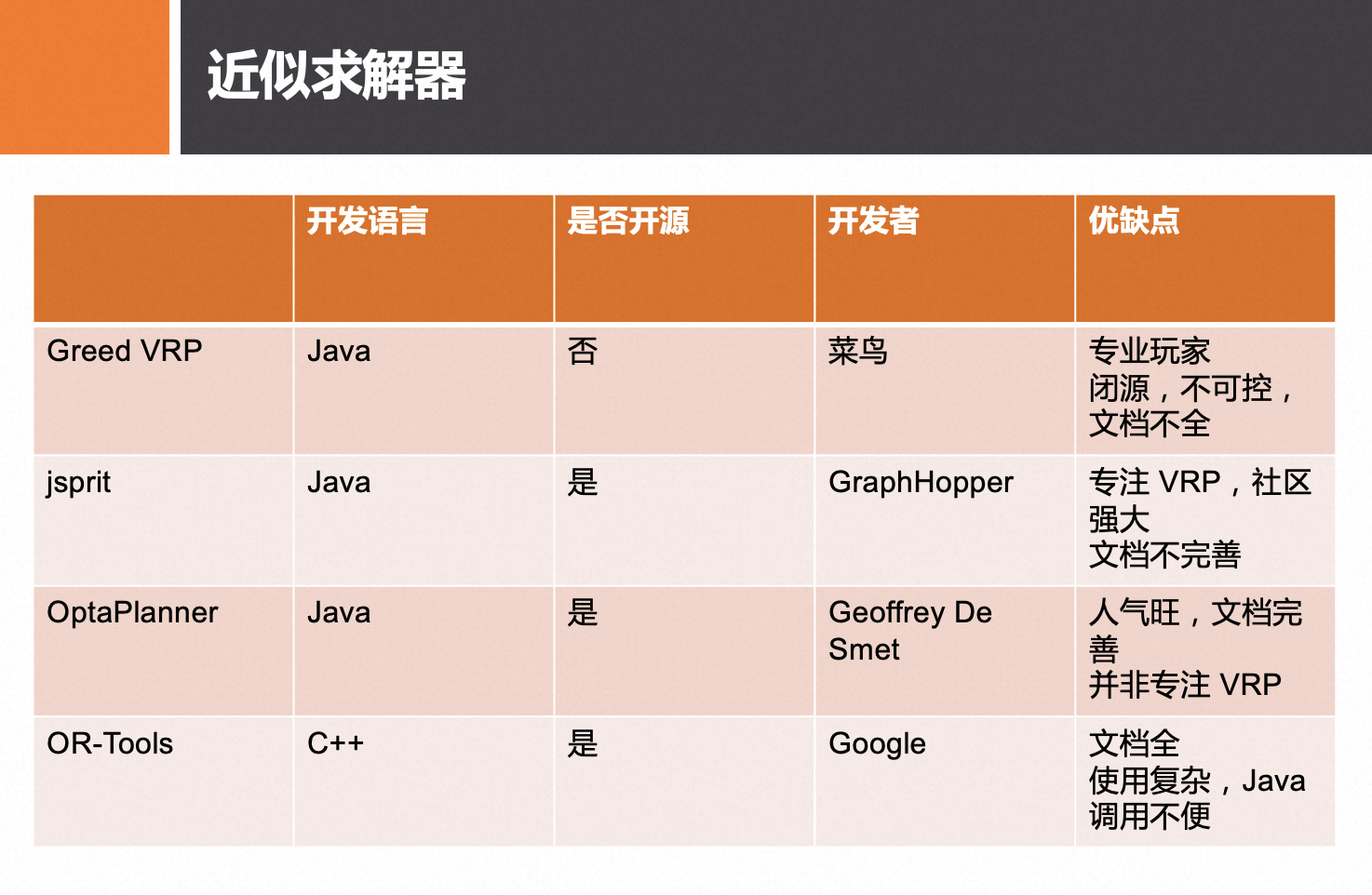
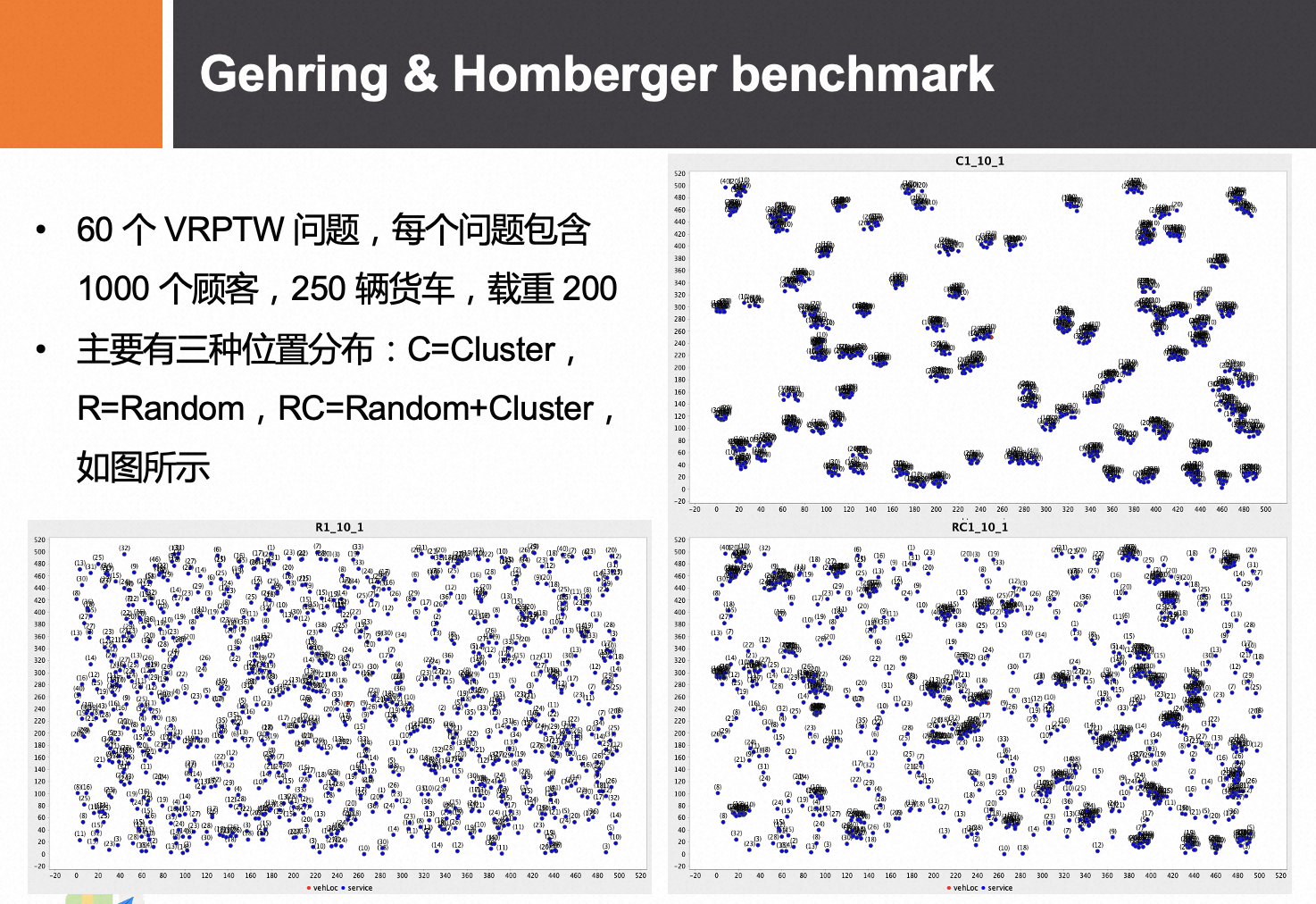
注：VRP 算法工具很多，此处仅列举 Top 部分

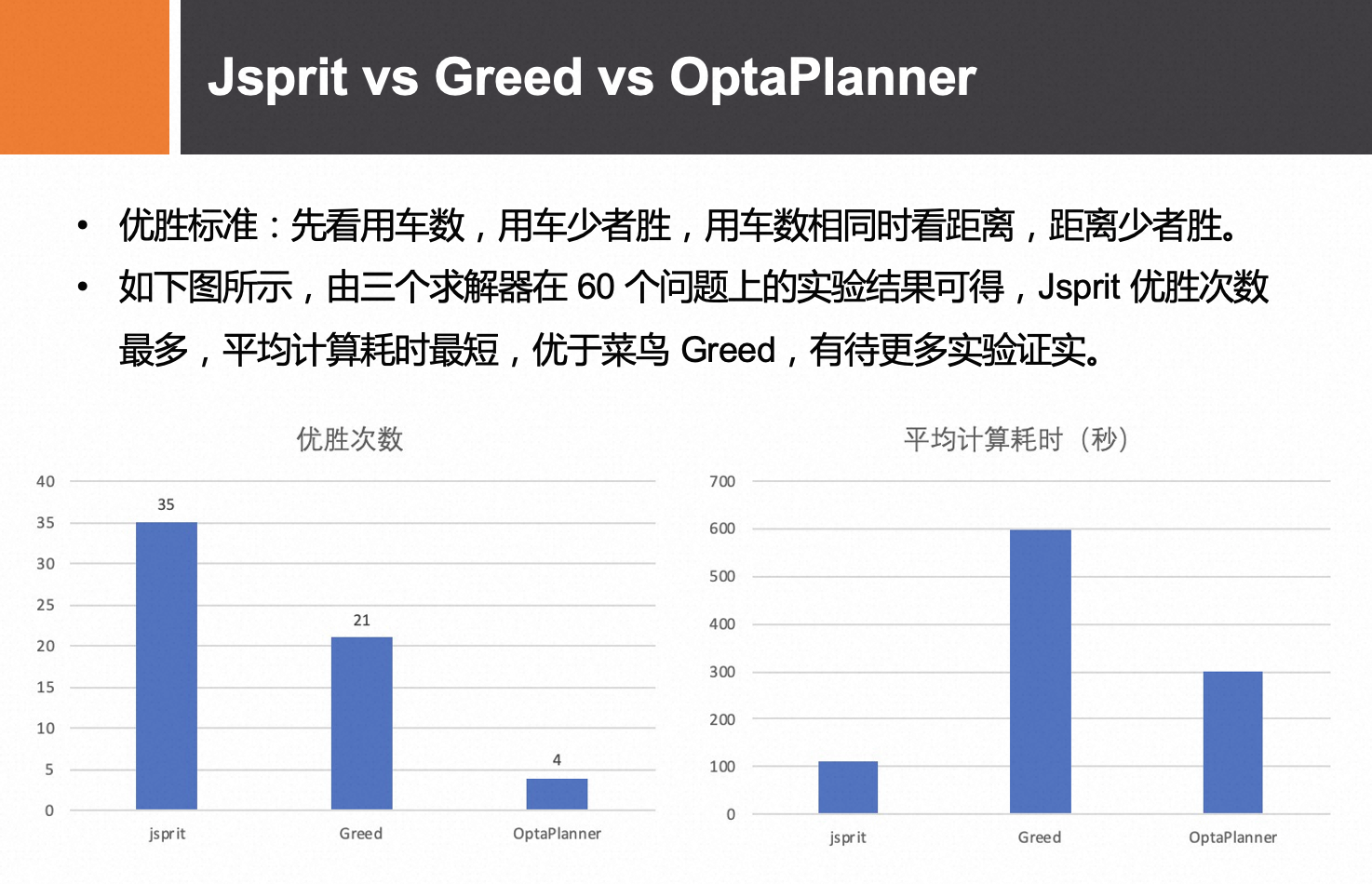
**注：以上为 2019 年 10 月在个人 mac 上的实验结果，各家版本更新后效果如何读者可做实验 **

参考文献

• The Truck Dispatching Problem
• The vehicle routing problem- State of the art classification and review
• Adaptive Large Neighborhood Search
• Branch and Bound Algorithms—Principles and Examples
• A general heuristic for vehicle routing problems
• Large neighborhood search
• The Pickup and Delivery Problem with Time Windows- an Adaptive Large Neighborhood Search heuristic